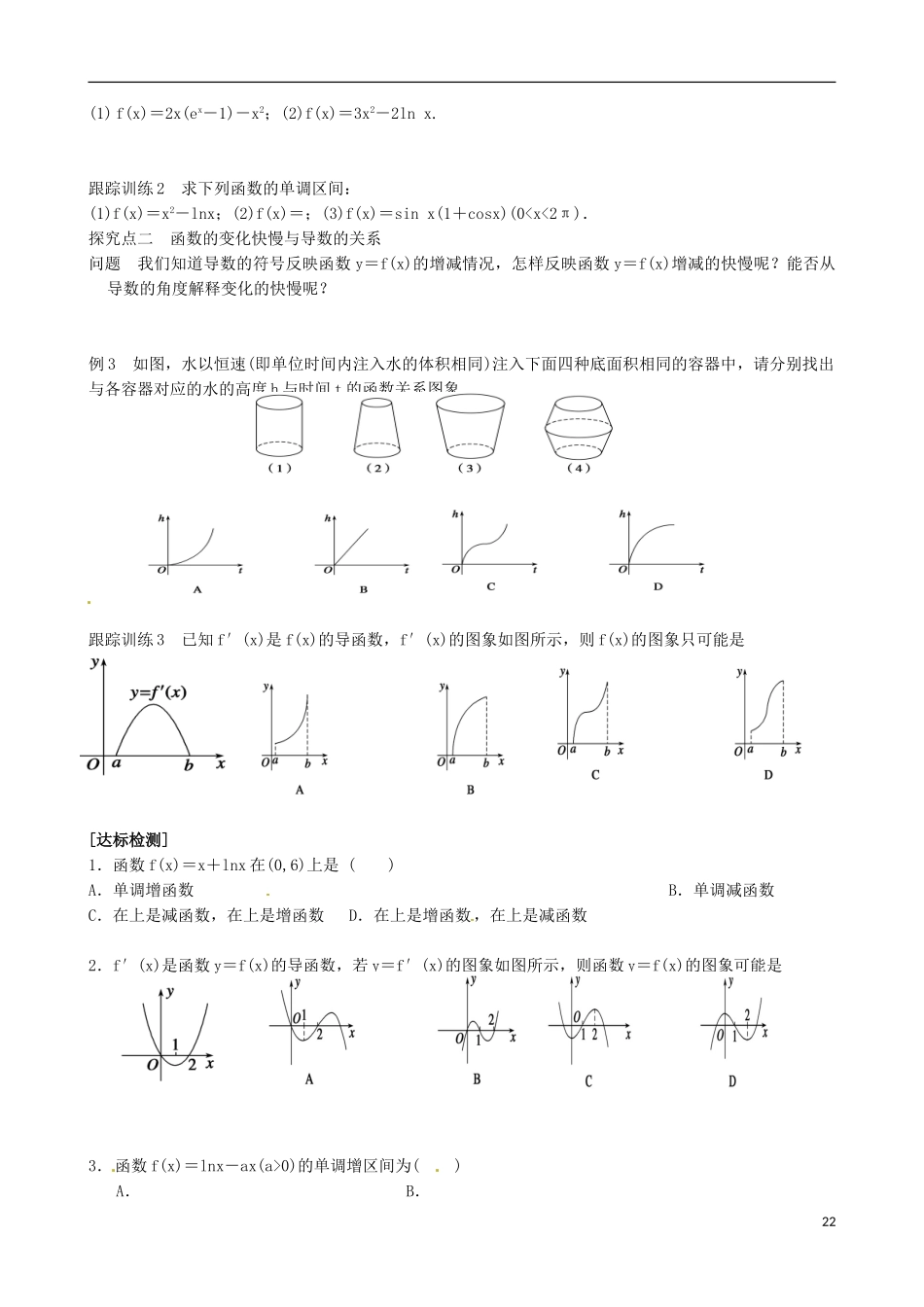
青海师范大学附属第二中学高中数学 1.3.1 函数的单调性与导数导学案 新人教 A 版选修 2-2[学习要求]1.结合实例,直观探索并掌握函数的单调性与导数的关系.2.能利用导数研究函数的单调性,并能够利用单调性证明一些简单的不等式.3.会求函数的单调区间(其中多项式函数一般不超过三次).[学法指导]结合函数图象(几何直观)探讨归纳函数的单调性与导函数正负之间的关系,体会数形结合思想,以直代曲思想.一般地,在区间(a,b)内函数的单调性与导数有如下关系:导数函数的单调性f′(x)>0单调递___f′(x)<0单调递___f′(x)=0常函数探究点一 函数的单调性与导函数正负的关系问题 1 观察高台跳水运动员的高度 h 随时间 t 变化的函数 h(t)=-4.9t2+6.5t+10 的图象,及 h′(t)=-9.8t+6.5 的图象,思考运动员从起跳到最高点,从最高点到入水的运动状态有什么区别.问题 2 观察下面四个函数的图象,回答函数的单调性与其导函数的正负有何关系?问题 3 若函数 f(x)在区间(a,b)内单调递增,那么 f′(x)一定大于零吗?问题 4 (1)如果一个函数具有相同单调性的单调区间不止一个,那么如何表示这些区间?试写出问题 2中(4)的单调区间.(2)函数的单调区间与其定义域满足什么关系?例 1 已知导函数 f′(x)的下列信息:当 10;当 x>4,或 x<1 时,f′(x)<0;当 x=4,或 x=1 时,f′(x)=0.试画出函数 f(x)图象的大致形状.跟踪训练 1 函数 y=f(x)的图象如图所示,试画出导函数 f′(x)图象的大致形状.例 2 求下列函数的单调区间:21(1) f(x)=2x(ex-1)-x2;(2)f(x)=3x2-2ln x.跟踪训练 2 求下列函数的单调区间:(1)f(x)=x2-lnx;(2)f(x)=;(3)f(x)=sin x(1+cosx)(0