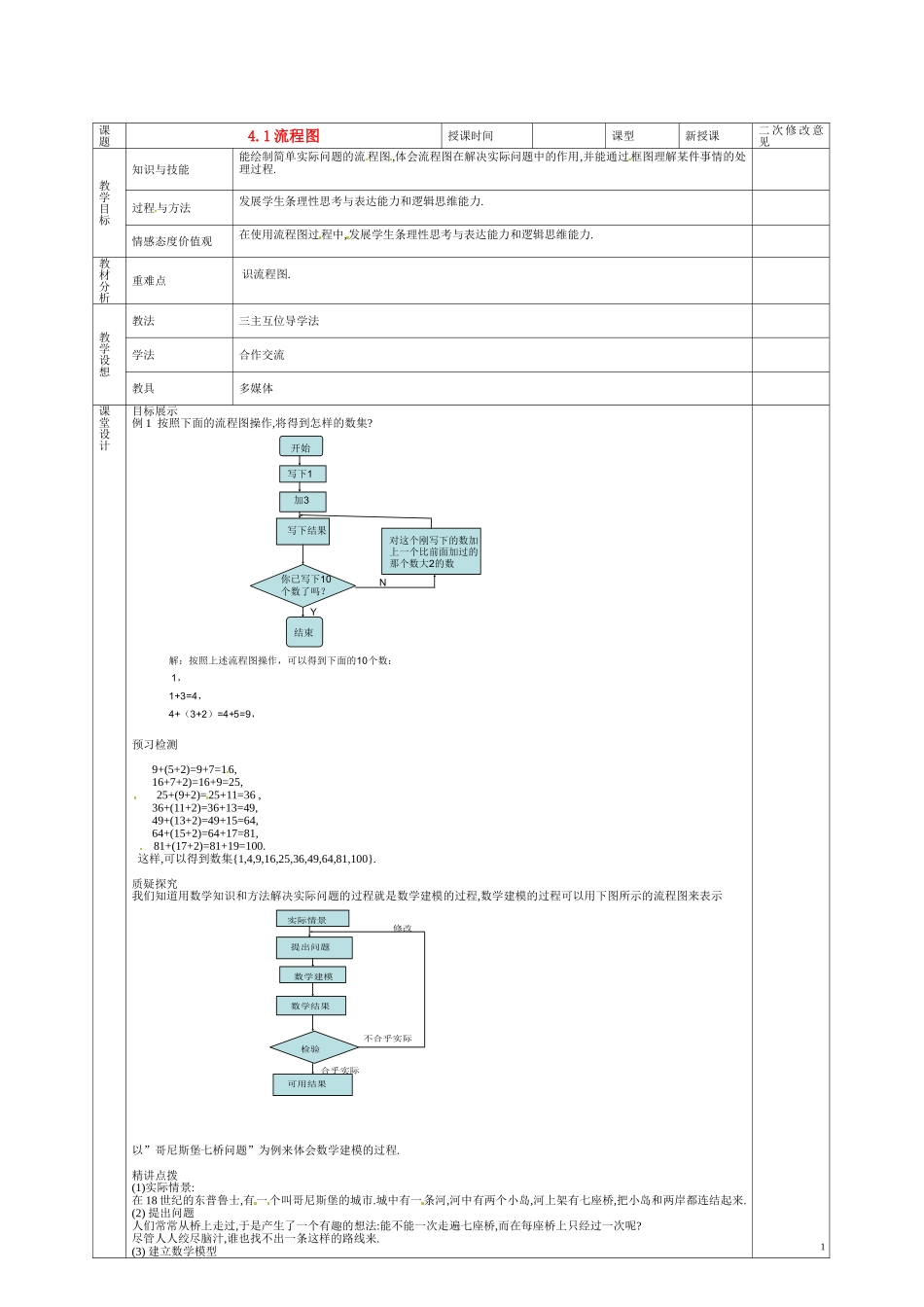
课题4.1 流程图授课时间课型新授课二 次 修 改 意见教学目标知识与技能能绘制简单实际问题的流 程图,体会流程图在解决实际问题中的作用,并能通过框图理解某件事情的处理过程.过程与方法发展学生条理性思考与表达能力和逻辑思维能力.情感态度价值观在使用流程图过程中,发展学生条理性思考与表达能力和逻辑思维能力.教材分析重难点 识流程图.教学设想教法三主互位导学法学法合作交流教具多媒体课堂设计目标展示例 1 按照下面的流程图操作,将得到怎样的数集?开始写下1加3写下结果你已写下10个数了吗?结束对这个刚写下的数加上一个比前面加过的那个数大2的数NY解:按照上述流程图操作,可以得到下面的10个数:1,1+3=4,4+(3+2)=4+5=9,预习检测 9+(5+2)=9+7=16, 16+7+2)=16+9=25, 25+(9+2)=25+11=36 , 36+(11+2)=36+13=49, 49+(13+2)=49+15=64, 64+(15+2)=64+17=81, 81+(17+2)=81+19=100. 这样,可以得到数集{1,4,9,16,25,36,49,64,81,100}.质疑探究我们知道用数学知识和方法解决实际问题的过程就是数学建模的过程,数学建模的过程可以用下图所示的流程图来表示实际情景提出问题数学建模数学结果检验可用结果合乎实际不合乎实际修改以”哥尼斯堡七桥问题”为例来体会数学建模的过程.精讲点拨(1)实际情景:在 18 世纪的东普鲁士,有一个叫哥尼斯堡的城市.城中有一条河,河中有两个小岛,河上架有七座桥,把小岛和两岸都连结起来.(2) 提出问题人们常常从桥上走过,于是产生了一个有趣的想法:能不能一次走遍七座桥,而在每座桥上只经过一次呢?尽管人人绞尽脑汁,谁也找不出一条这样的路线来.(3) 建立数学模型11736 年,这事传到了瑞士 大数学家欧拉的耳里,他立刻对这个问题产生了兴趣,动手研究起来.作为一个数学家,他的 研究方法和一般人不同,他没有到桥上去走走,而是将具体问题转化为一个数学模型. 欧拉用点代表两岸和小岛,用线代表桥,于是上面的问题就转化为能否一笔画出图中的网络图形,即”一笔画”问题,所谓” 一笔画”,通俗的说,就是笔不离开纸面,能不重复的画出网络图形中的每一条线.(4)得到数学结果:在”一笔画”问题 中,如果一个点不是起点和终点,那么有一条走向它的线,就必须有另一条离开它的线.就是说,连结着点的线条数目是偶数,这种点成为偶点.如果连结一个点的数目是奇数,那么这种点成为奇点,显然奇点只能作为起点或终点. 因此,能够一笔画出一个网络图形的条件,就是它要么没有奇点,要么最多只有两个奇 点,(分别作为起...