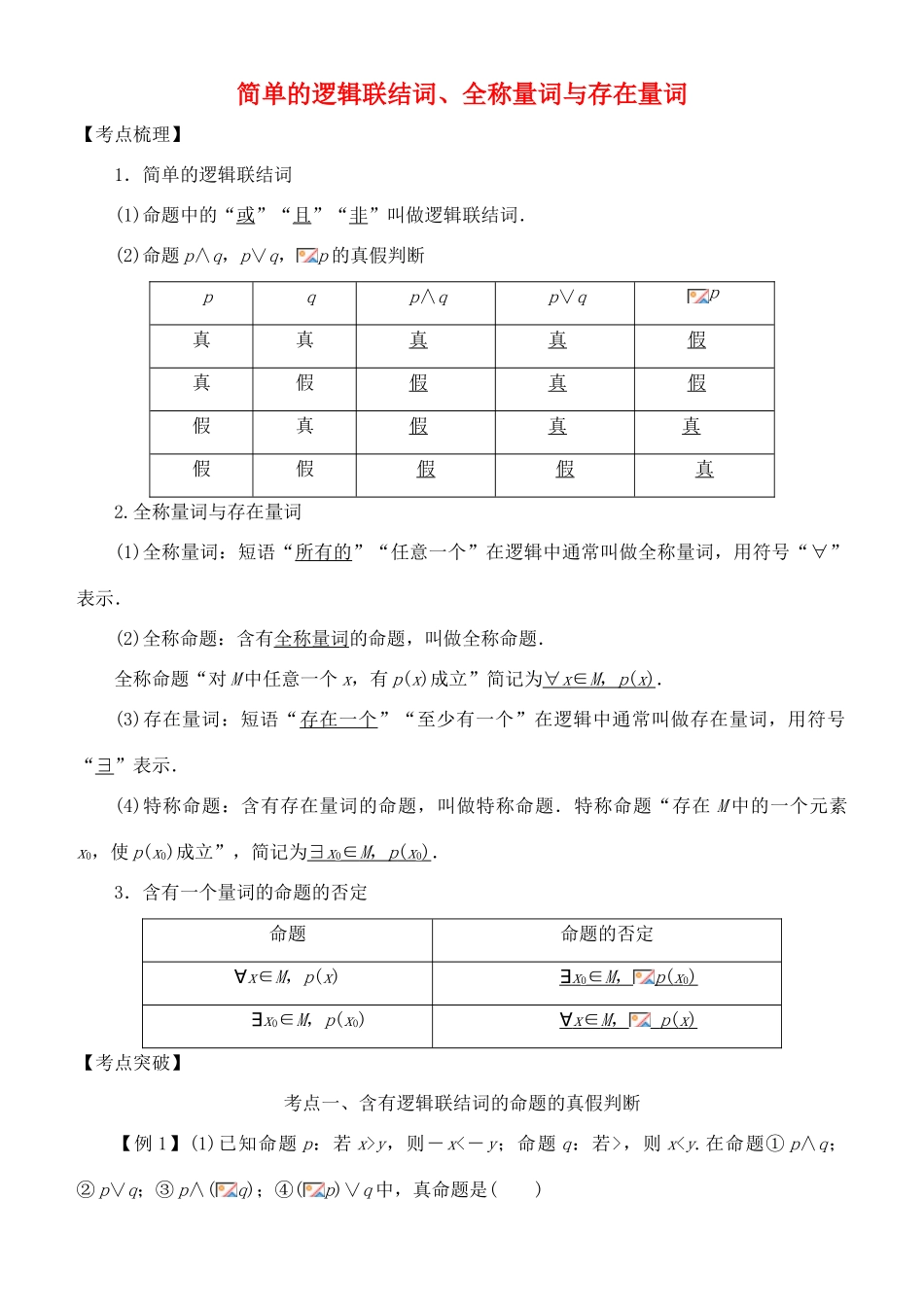
简单的逻辑联结词、全称量词与存在量词【考点梳理】1.简单的逻辑联结词(1)命题中的“或”“且”“非”叫做逻辑联结词.(2)命题 p∧q,p∨q,p 的真假判断pqp∧qp∨qp真真真真假真假假真假假真假真 真假假假假真2.全称量词与存在量词(1)全称量词:短语“所有的”“任意一个”在逻辑中通常叫做全称量词,用符号“∀”表示.(2)全称命题:含有全称量词的命题,叫做全称命题.全称命题“对 M 中任意一个 x,有 p(x)成立”简记为∀ x ∈ M , p ( x ) .(3)存在量词:短语“存在一个”“至少有一个”在逻辑中通常叫做存在量词,用符号“∃”表示.(4)特称命题:含有存在量词的命题,叫做特称命题.特称命题“存在 M 中的一个元素x0,使 p(x0)成立”,简记为∃ x 0∈ M , p ( x 0).3.含有一个量词的命题的否定命题命题的否定∀x∈M,p(x)∃ x 0∈ M , p ( x 0)∃x0∈M,p(x0)∀ x ∈ M , p ( x ) 【考点突破】考点一、含有逻辑联结词的命题的真假判断【例 1】(1)已知命题 p:若 x>y,则-x<-y;命题 q:若>,则 x3;命题 q:∀x∈(2,+∞),x2>2x,则下列命题为真的是( )A.p∧(q) B.(p)∧qC.p∧q D.(p)∨q[答案] (1)C (2)A[解析] (1) 由不等式的性质可知,命题 p 是真命题,命题 q 为假命题,故① p∧q 为假命题;② p∨q 为真命题;③q 为真命题,则 p∧(q)为真命题;④p 为假命题,则(p)∨q 为假命题.(2) 对于命题 p,当 x0=4 时,x0+=>3,故命题 p 为真命题;对于命题 q,当 x=4 时,24=42=16,即∃x0∈(2,+∞),使得 2x0=x 成立,故命题 q 为假命题,所以 p∧(q)为真命题,故选 A.【类题通法】1.判断含有逻辑联结词命题真假的步骤2.p 且 q 形式是“一假必假,全真才真”,p 或 q 形式是“一真必真,全假才假”,非 p则是“与 p 的真假相反”.【对点训练】1.已知命题 p:a2≥0(a∈R),命题 q:函数 f(x)=x2-x 在区间[0,+∞)上单调递增,则下列命题:①p∨q;② p∧q;③(p)∧(q);④(p)∨q.其中为假命题的序号为________.[答案] ②③④[解析] 显然命题 p 为真命题,p 为假命题. f(x)=x2-x=2-,∴函数 f(x)在区间上单调递增.∴命题 q 为假命题,q 为真命题...