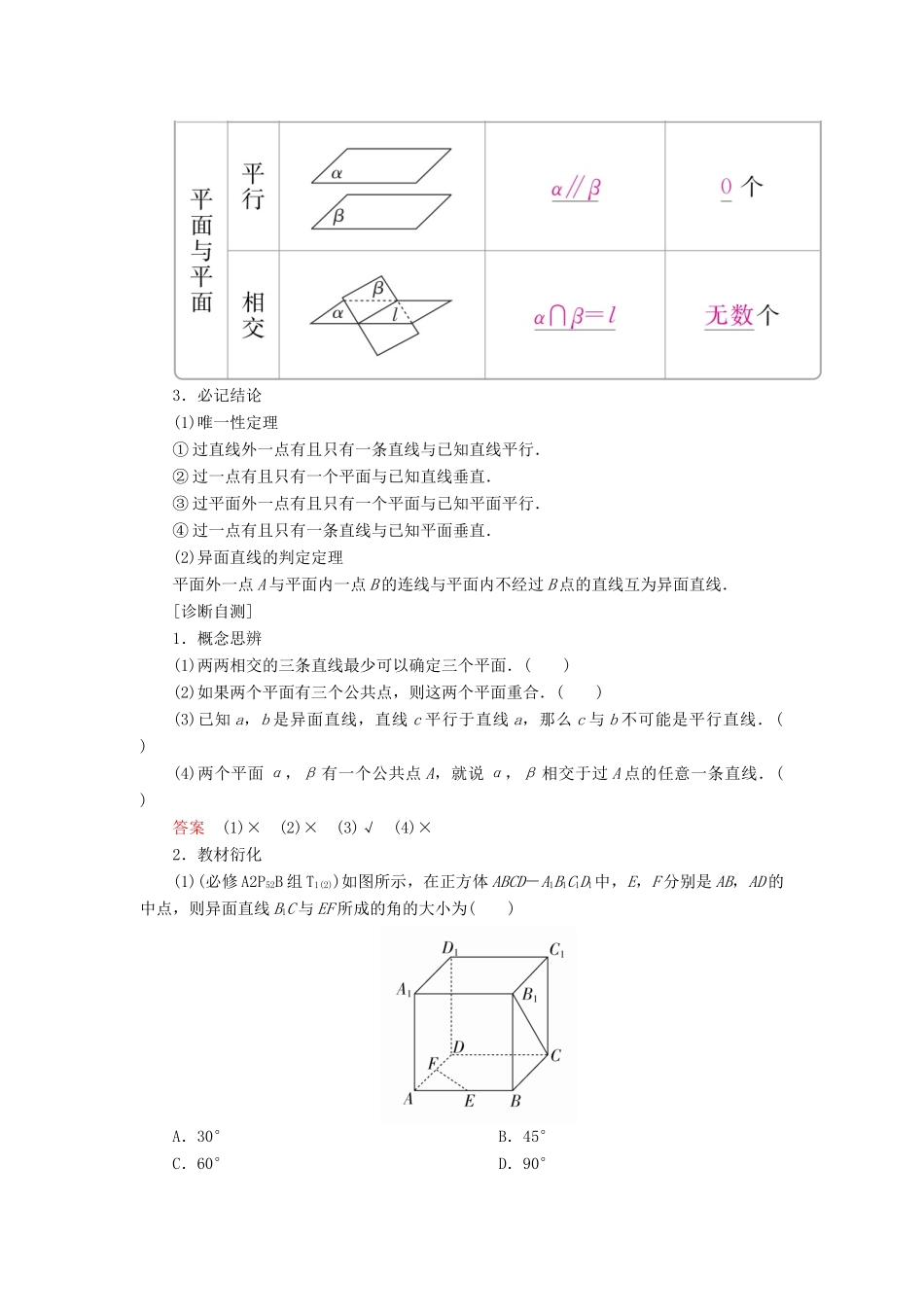
7.3 空间点、直线、平面之间的位置关系[知识梳理]1.空间两条直线的位置关系(1)位置关系分类:(2)异面直线所成的角① 定义:设 a,b 是两条异面直线,经过空间任一点 O 作直线 a′∥a,b′∥b,把 a′与 b′所成的锐角 ( 或直角 ) 叫做异面直线 a 与 b 所成的角(或夹角).② 范围:.(3)等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.2.空间直线与平面、平面与平面的位置关系3.必记结论(1)唯一性定理① 过直线外一点有且只有一条直线与已知直线平行.② 过一点有且只有一个平面与已知直线垂直.③ 过平面外一点有且只有一个平面与已知平面平行.④ 过一点有且只有一条直线与已知平面垂直.(2)异面直线的判定定理平面外一点 A 与平面内一点 B 的连线与平面内不经过 B 点的直线互为异面直线.[诊断自测]1.概念思辨(1)两两相交的三条直线最少可以确定三个平面.( )(2)如果两个平面有三个公共点,则这两个平面重合.( )(3)已知 a,b 是异面直线,直线 c 平行于直线 a,那么 c 与 b 不可能是平行直线.( )(4)两个平面 α,β 有一个公共点 A,就说 α,β 相交于过 A 点的任意一条直线.( )答案 (1)× (2)× (3)√ (4)×2.教材衍化(1)(必修 A2P52B 组 T1(2))如图所示,在正方体 ABCD-A1B1C1D1中,E,F 分别是 AB,AD 的中点,则异面直线 B1C 与 EF 所成的角的大小为( )A.30° B.45°C.60° D.90°答案 C解析 连接 B1D1,D1C,则 B1D1∥EF,故∠D1B1C 为所求的角.又 B1D1=B1C=D1C,所以∠D1B1C=60°.故选 C.(2)(必修 A2P63B 组 T1)在四棱锥 P-ABCD 中,底面 ABCD 为平行四边形,E,F 分别为侧棱 PC,PB 的中点,则 EF 与平面 PAD 的位置关系为________,平面 AEF 与平面 ABCD 的交线是________.答案 平行 AD解析 E,F 分别为 PC,PB 中点,所以 EF∥BC,又 BC∥AD.所以 EF∥AD,而 AD⊂平面 PAD,EF⊄平面 PAD.所以 EF∥平面 PAD.由上述推证易得两面交线为 AD.3.小题热身(1)(2016·山东高考)已知直线 a,b 分别在两个不同的平面 α,β 内,则“直线 a 和直线 b 相交”是“平面 α 和平面 β 相交”的( )A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件答案 A解析 由题意知 a⊂α,b⊂β,若 a,b 相交,则 a,b 有公共点,从而 α,β 有公共...