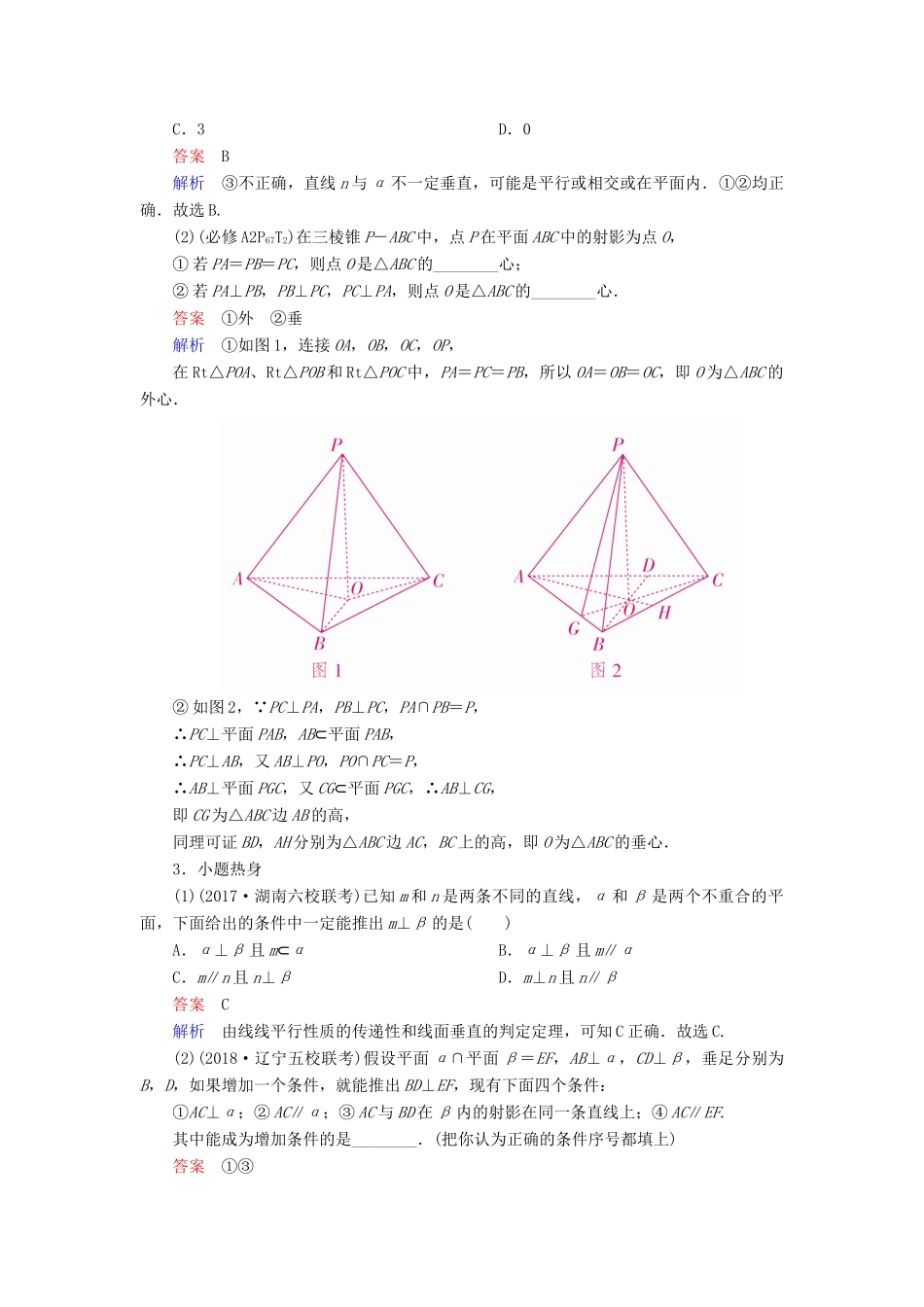
7.5 直线、平面垂直的判定与性质[知识梳理]1.直线与平面垂直判定定理与性质定理2.平面与平面垂直判定定理与性质定理3.直线和平面所成的角范围:.4.二面角范围[0 , π] . 5.必记结论(1)若两条平行线中一条垂直于一个平面,则另一条也垂直于这个平面.(2)若一条直线垂直于一个平面,则这条直线垂直于这个平面内任何一条直线.(3)过空间任一点有且只有一条直线与已知平面垂直.(4)过空间任一点有且只有一个平面与已知直线垂直.(5)两平面垂直的性质定理是把面面垂直转化为线面垂直.(6)两个相交平面同时垂直于第三个平面,它们的交线也垂直于第三个平面.[诊断自测]1.概念思辨(1)直线 l 与平面 α 内的无数条直线都垂直,则 l⊥α.( )(2)垂直于同一个平面的两平面平行.( )(3)若两平面垂直,则其中一个平面内的任意一条直线垂直于另一个平面.( )(4)若平面 α 内的一条直线垂直于平面 β 内的无数条直线,则 α⊥β.( )答案 (1)× (2)× (3)× (4)×2.教材衍化(1)(必修 A2P73A 组 T1)若 m,n 表示两条不同的直线,α 表示平面,则下列命题中,正确命题的个数为( )①⇒m∥n;②⇒m⊥n;③⇒n⊥α.A.1 B.2 C.3 D.0答案 B解析 ③不正确,直线 n 与 α 不一定垂直,可能是平行或相交或在平面内.①②均正确.故选 B.(2)(必修 A2P67T2)在三棱锥 P-ABC 中,点 P 在平面 ABC 中的射影为点 O,① 若 PA=PB=PC,则点 O 是△ABC 的________心;② 若 PA⊥PB,PB⊥PC,PC⊥PA,则点 O 是△ABC 的________心.答案 ①外 ②垂解析 ①如图 1,连接 OA,OB,OC,OP,在 Rt△POA、Rt△POB 和 Rt△POC 中,PA=PC=PB,所以 OA=OB=OC,即 O 为△ABC 的外心.② 如图 2, PC⊥PA,PB⊥PC,PA∩PB=P,∴PC⊥平面 PAB,AB⊂平面 PAB,∴PC⊥AB,又 AB⊥PO,PO∩PC=P,∴AB⊥平面 PGC,又 CG⊂平面 PGC,∴AB⊥CG,即 CG 为△ABC 边 AB 的高,同理可证 BD,AH 分别为△ABC 边 AC,BC 上的高,即 O 为△ABC 的垂心.3.小题热身(1)(2017·湖南六校联考)已知 m 和 n 是两条不同的直线,α 和 β 是两个不重合的平面,下面给出的条件中一定能推出 m⊥β 的是( )A.α⊥β 且 m⊂α B.α⊥β 且 m∥αC.m∥n 且 n⊥β D.m⊥n 且 n∥β答案 C解析 由线线平行性质的传递性和线面垂直的判定定理,可知 C 正确.故选 C.(2)(2018·...