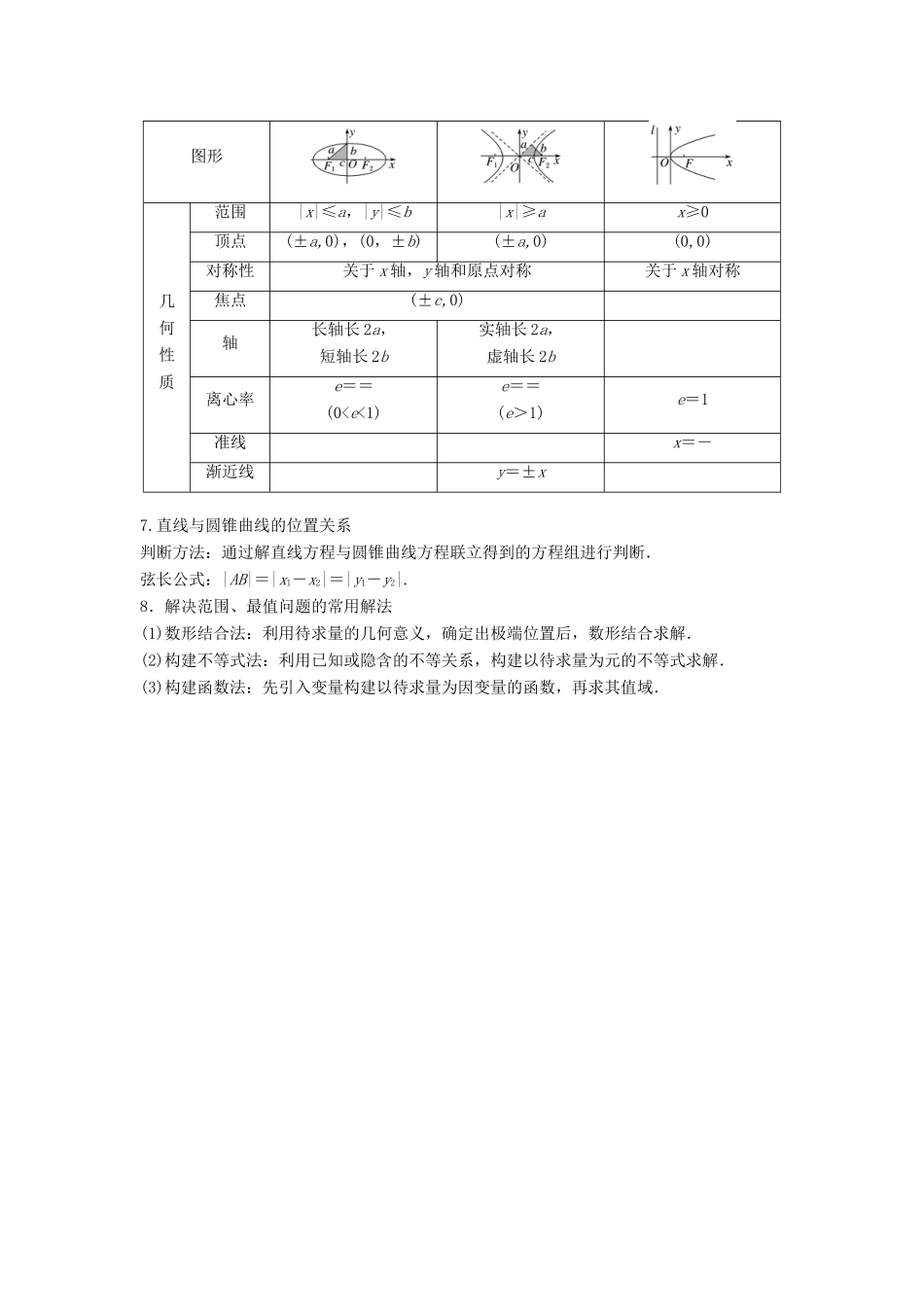
回扣 8 解析几何1.直线方程的五种形式(1)点斜式:y-y1=k(x-x1)(直线过点 P1(x1,y1),且斜率为 k,不包括 y 轴和平行于 y 轴的直线).(2)斜截式:y=kx+b(b 为直线 l 在 y 轴上的截距,且斜率为 k,不包括 y 轴和平行于 y 轴的直线).(3)两点式:=(直线过点 P1(x1,y1),P2(x2,y2),且 x1≠x2,y1≠y2,不包括坐标轴和平行于坐标轴的直线).(4)截距式:+=1(a,b 分别为直线的横、纵截距,且 a≠0,b≠0,不包括坐标轴、平行于坐标轴和过原点的直线).(5)一般式:Ax+By+C=0(其中 A,B 不同时为 0).2.直线的两种位置关系当不重合的两条直线 l1和 l2的斜率存在时:(1)两直线平行 l1∥l2⇔k1=k2.(2)两直线垂直 l1⊥l2⇔k1·k2=-1.提醒 当一条直线的斜率为 0,另一条直线的斜率不存在时,两直线也垂直,此种情形易忽略.3.三种距离公式(1)A(x1,y1),B(x2,y2)两点间的距离|AB|=.(2)点到直线的距离 d=(其中点 P(x0,y0),直线方程为 Ax+By+C=0).(3)两平行线间的距离 d=(其中两平行线方程分别为 l1:Ax+By+C1=0,l2:Ax+By+C2=0).提醒 应用两平行线间距离公式时,注意两平行线方程中 x,y 的系数应对应相等.4.圆的方程的两种形式(1)圆的标准方程:(x-a)2+(y-b)2=r2.(2)圆的一般方程:x2+y2+Dx+Ey+F=0(D2+E2-4F>0).5.直线与圆、圆与圆的位置关系(1)直线与圆的位置关系:相交、相切、相离,代数判断法与几何判断法.(2)圆与圆的位置关系:相交、内切、外切、外离、内含,代数判断法与几何判断法.6.圆锥曲线的定义、标准方程与几何性质名称椭圆双曲线抛物线定义|PF1|+|PF2|=2a(2a>|F1F2|)||PF1|-|PF2||=2a(2a<|F1F2|)|PF|=|PM|点 F 不在直线 l 上,PM⊥l 于 M标准方程+=1(a>b>0)-=1(a>0,b>0)y2=2px(p>0)图形几何性质范围|x|≤a,|y|≤b|x|≥ax≥0顶点(±a,0),(0,±b)(±a,0)(0,0)对称性关于 x 轴,y 轴和原点对称关于 x 轴对称焦点(±c,0)轴长轴长 2a,短轴长 2b实轴长 2a,虚轴长 2b离心率e==(0