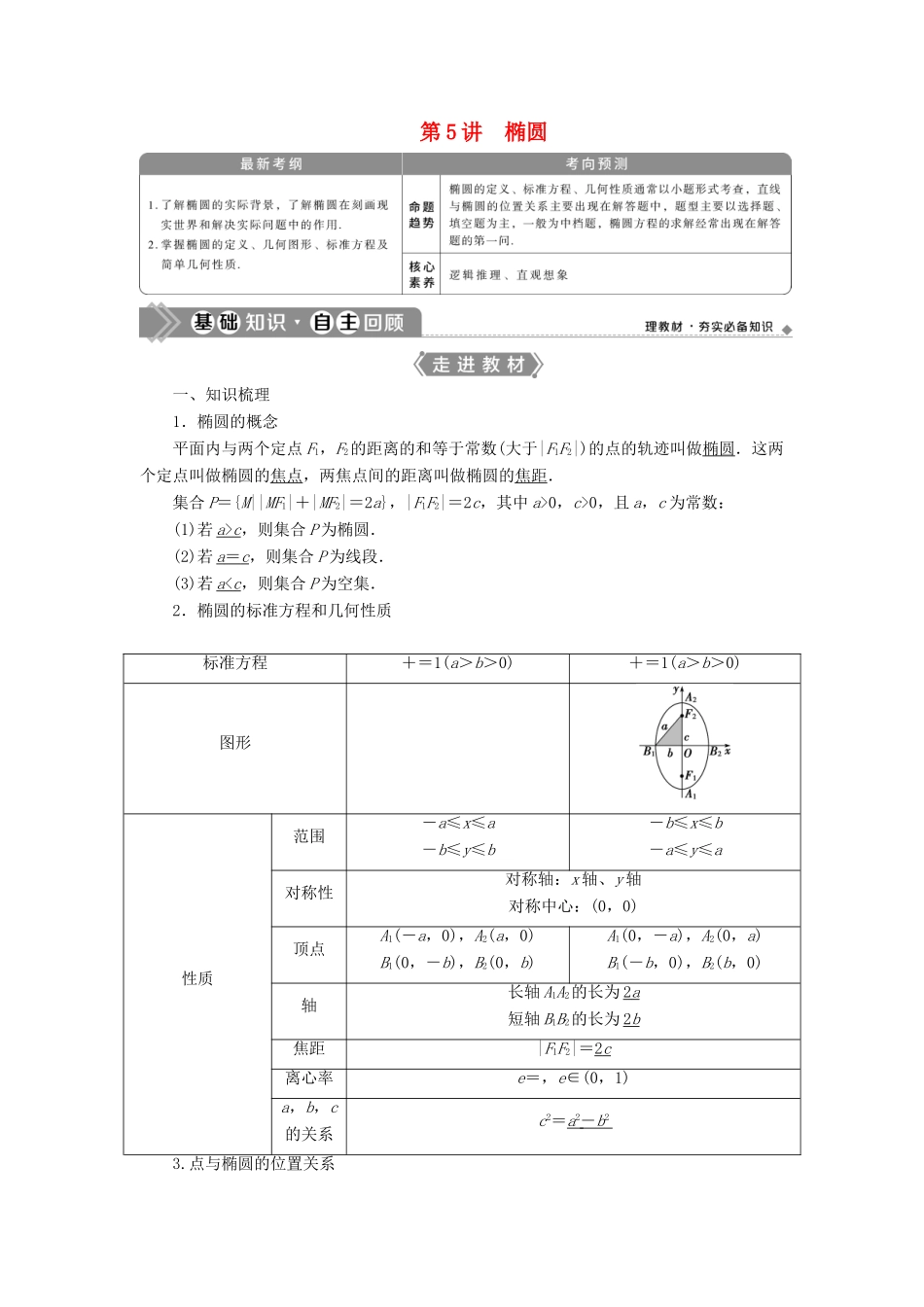
第 5 讲 椭圆一、知识梳理1.椭圆的概念平面内与两个定点 F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.集合 P={M||MF1|+|MF2|=2a},|F1F2|=2c,其中 a>0,c>0,且 a,c 为常数:(1)若 a > c ,则集合 P 为椭圆.(2)若 a = c ,则集合 P 为线段.(3)若 a < c ,则集合 P 为空集.2.椭圆的标准方程和几何性质标准方程+=1(a>b>0)+=1(a>b>0)图形性质范围-a≤x≤a-b≤y≤b-b≤x≤b-a≤y≤a对称性对称轴:x 轴、y 轴对称中心:(0,0)顶点A1(-a,0),A2(a,0)B1(0,-b),B2(0,b)A1(0,-a),A2(0,a)B1(-b,0),B2(b,0)轴长轴 A1A2的长为 2 a 短轴 B1B2的长为 2 b 焦距|F1F2|=2 c 离心率e=,e∈(0,1)a,b,c的关系c2=a 2 - b 2 3.点与椭圆的位置关系已知点 P(x0,y0),椭圆+=1(a>b>0),则(1)点 P(x0,y0)在椭圆内⇔+<1.(2)点 P(x0,y0)在椭圆上⇔+=1.(3)点 P(x0,y0)在椭圆外⇔+>1.常用结论(1)焦半径:椭圆上的点 P(x0,y0)与左(下)焦点 F1与右(上)焦点 F2之间的线段的长度叫作椭圆的焦半径,分别记作 r1=|PF1|,r2=|PF2|.①+=1(a>b>0),r1=a+ex0,r2=a-ex0;②+=1(a>b>0),r1=a+ey0,r2=a-ey0;③ 焦半径中以长轴端点的焦半径最大和最小(近日点与远日点).(2)焦点三角形:椭圆上的点 P(x0,y0)与两焦点构成的△PF1F2叫作焦点三角形.r1=|PF1|,r2=|PF2|,∠F1PF2=θ,△PF1F2的面积为 S,则在椭圆+=1(a>b>0)中:① 当 r1=r2时,即点 P 的位置为短轴端点时,θ 最大;②S=b2tan =c|y0|,当|y0|=b 时,即点 P 的位置为短轴端点时,S 取最大值,最大值为 bc.(3)焦点弦(过焦点的弦):焦点弦中以通径(垂直于长轴的焦点弦)最短,弦长 lmin=.(4)AB 为椭圆+=1(a>b>0)的弦,A(x1,y1),B(x2,y2),弦中点 M(x0,y0),则① 弦长 l=|x1-x2|=|y1-y2|;② 直线 AB 的斜率 kAB=-.二、教材衍化1.若 F1(-3,0),F2(3,0),点 P 到 F1,F2 距离之和为 10,则 P 点的轨迹方程是( )A.+=1 B.+=1C.+=1 D.+=1 或+=1解析:选 A.设点 P 的坐标为(x,y),因为|PF1|+|PF2|=10>|F1F2|=6,所以点 P 的轨迹是以 F1,F2为焦点的椭圆,其中 a=5,c=3,b==4,故点 P 的轨迹方程为+=1.故选A.2.设椭圆的两个焦点分别...