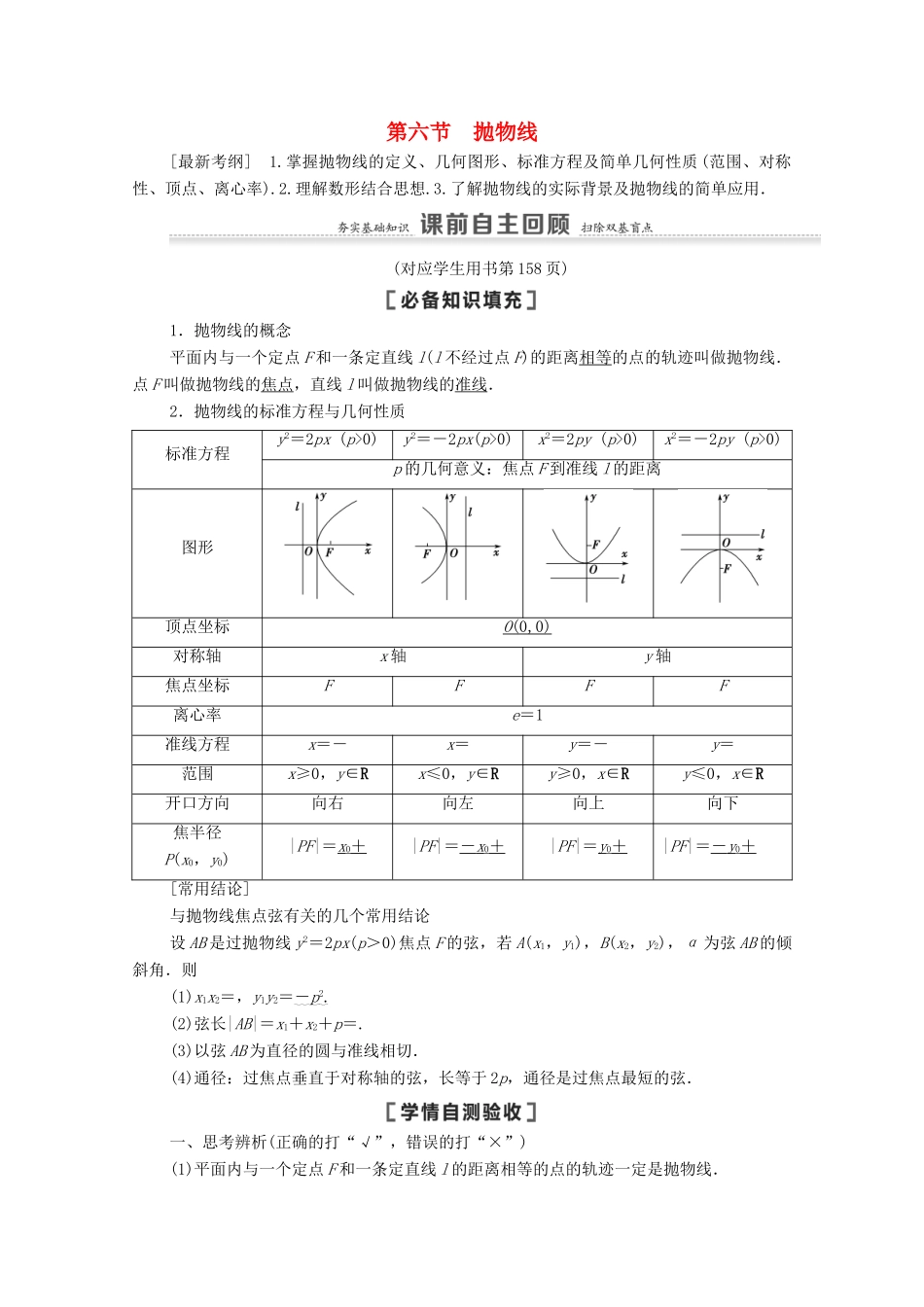
第六节 抛物线[最新考纲] 1.掌握抛物线的定义、几何图形、标准方程及简单几何性质 (范围、对称性、顶点、离心率).2.理解数形结合思想.3.了解抛物线的实际背景及抛物线的简单应用.(对应学生用书第 158 页)1.抛物线的概念平面内与一个定点 F 和一条定直线 l(l 不经过点 F)的距离相等的点的轨迹叫做抛物线.点 F 叫做抛物线的焦点,直线 l 叫做抛物线的准线.2.抛物线的标准方程与几何性质标准方程y2=2px (p>0)y2=-2px(p>0)x2=2py (p>0)x2=-2py (p>0)p 的几何意义:焦点 F 到准线 l 的距离图形顶点坐标O (0,0) 对称轴x 轴y 轴焦点坐标FFFF离心率e=1准线方程x=-x=y=-y=范围x≥0,y∈Rx≤0,y∈Ry≥0,x∈Ry≤0,x∈R开口方向向右向左向上向下焦半径P(x0,y0)|PF|=x0+|PF|=- x 0+|PF|=y0+|PF|=- y 0+[常用结论]与抛物线焦点弦有关的几个常用结论设 AB 是过抛物线 y2=2px(p>0)焦点 F 的弦,若 A(x1,y1),B(x2,y2),α 为弦 AB 的倾斜角.则(1)x1x2=,y1y2=- p 2 .(2)弦长|AB|=x1+x2+p=.(3)以弦 AB 为直径的圆与准线相切.(4)通径:过焦点垂直于对称轴的弦,长等于 2p,通径是过焦点最短的弦.一、思考辨析(正确的打“√”,错误的打“×”)(1)平面内与一个定点 F 和一条定直线 l 的距离相等的点的轨迹一定是抛物线.( )(2)抛物线 y2=4x 的焦点到准线的距离是 4.( )(3)抛物线既是中心对称图形,又是轴对称图形.( )(4)方程 y=ax2(a≠0)表示的曲线是焦点在 x 轴上的抛物线,且其焦点坐标是,准线方程是 x=-.( )[答案](1)× (2)× (3)× (4)×二、教材改编1.抛物线 y=x2的准线方程是( )A.y=-1 B.y=-2C.x=-1D.x=-2A [ y=x2,∴x2=4y,∴准线方程为 y=-1.]2.若抛物线 y=4x2上的一点 M 到焦点的距离为 1,则点 M 的纵坐标是( )A. B. C. D.0B [M 到准线的距离等于 M 到焦点的距离,又准线方程为 y=-,设 M(x,y),则 y+=1,∴y=.]3.过抛物线 y2=4x 的焦点的直线 l 交抛物线于 P(x1,y1),Q(x2,y2)两点,如果 x1+x2=6,则|PQ|等于( )A.9B.8 C.7D.6B [抛物线 y2=4x 的焦点为 F(1,0),准线方程为 x=-1.根据题意可得,|PQ|=|PF|+|QF|=x1+1+x2+1=x1+x2+2=8.]4.已知抛物线的顶点是原点,对称轴为坐标轴,并且经过点 P(-2,-4),则该抛物线的标准方程为________....