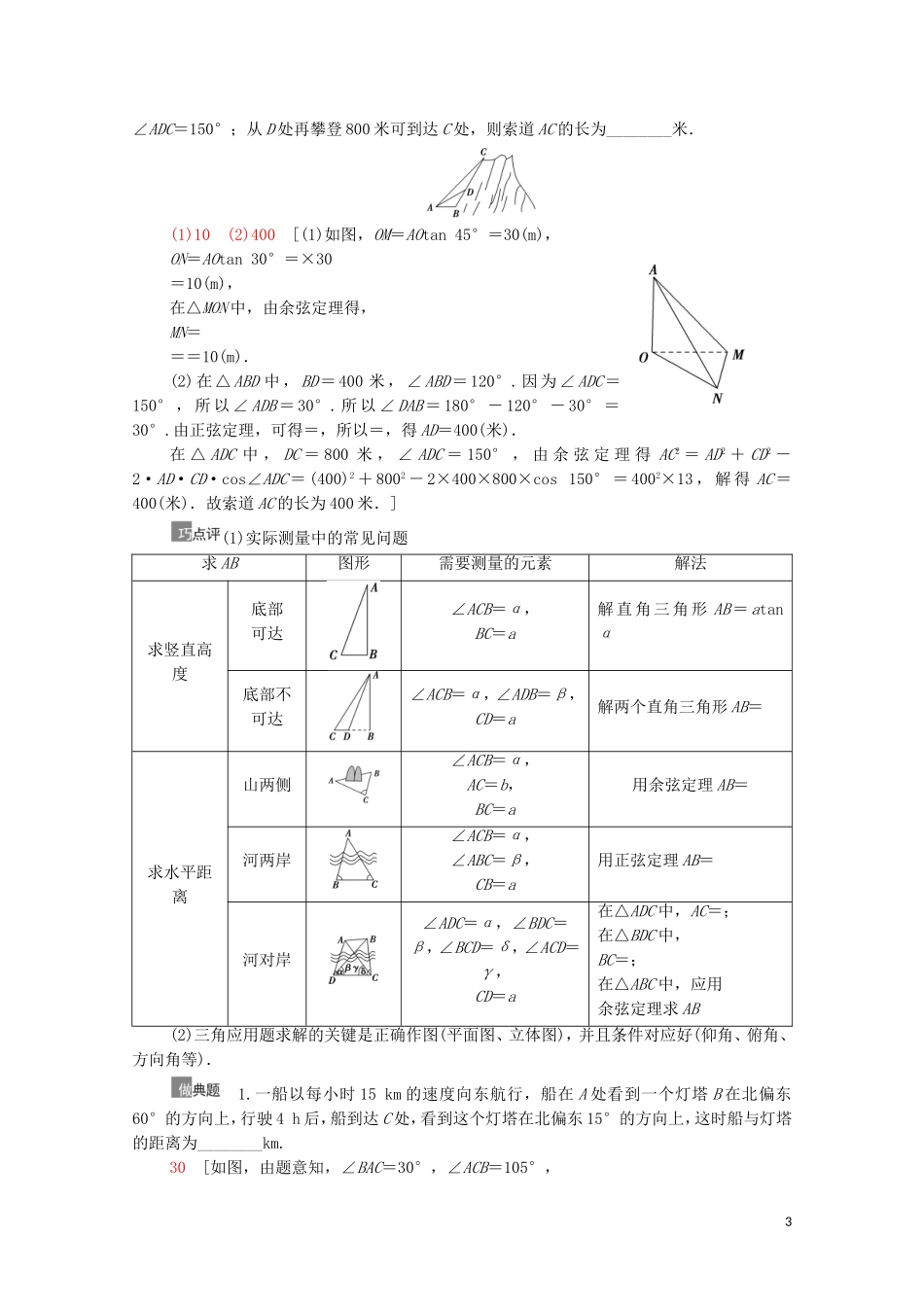
第七节 解三角形的实际应用举例[最新考纲] 能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题.(对应学生用书第 78 页)测量中的几个有关术语术语名称术语意义图形表示仰角与俯角在目标视线与水平视线所成的角中,目标视线在水平视线上方的叫做仰角,目标视线在水平视线下方的叫做俯角方位角从某点的指北方向线起按顺时针方向到目标方向线之间的夹角叫做方位角.方位角 θ 的范围是 0°≤θ<360°方向角相对于某正方向的水平角,如北偏东α,即由正北方向顺时针旋转 α 到达目标方向,南偏西 α,即由正南方向顺时针旋转 α 到达目标方向,其他方向角类似例:(1)北偏东 α:(2)南偏西 α:一、思考辨析(正确的打“√”,错误的打“×”)(1)从 A 处望 B 处的仰角为 α,从 B 处望 A 处的俯角为 β,则 α,β 的关系为 α+β=180°.( )(2)俯角是铅垂线与视线所成的角,其范围为.( )(3)方位角与方向角其实质是一样的,均是确定观察点与目标点之间的位置关系.( )(4)方位角大小的范围是[0,2π),方向角大小的范围一般是.( )[答案](1)× (2)× (3)√ (4)√二、教材改编1.如图所示,设 A,B 两点在河的两岸,一测量者在 A 所在的同侧河岸边选定一点 C,测出AC 的距离为 50 m,∠ACB=45°,∠CAB=105°后,就可以计算出 A,B 两点的距离为1________m.50 [由正弦定理得=,又 B=30°,∴AB===50(m).]2.如图,在山脚 A 测得山顶 P 的仰角为 30°,沿倾斜角为 15°的斜坡向上走 a 米到 B,在B 处测得山顶 P 的仰角为 60°,则山高 h=________米.a [由题图可得∠PAQ=α=30°,∠BAQ=β=15°,△PAB 中,∠PAB=α-β=15°,又∠PBC=γ=60°,∴∠BPA=(90°-α)-(90°-γ)=γ-α=30°,∴=,∴PB=a,∴PQ=PC+CQ=PB·sin γ+asin β=a×sin 60°+asin 15°=a.]3.如图所示,D,C,B 三点在地面的同一条直线上,DC=a,从 C,D 两点测得 A 点的仰角分别为 60°,30°,则 A 点离地面的高度 AB=________.a [由已知得∠DAC=30°,△ADC 为等腰三角形,AC=a,所以在 Rt△ACB 中,AB=AC·sin∠ACB=a.](对应学生用书第 79 页)⊙考点 1 解三角形中的实际问题 利用正、余弦定理解决实际问题的一般步骤(1)分析——理解题意,分清已知与未知,画出示意图.(2)建模——根据已知条件与求解目标,把已知量与求...