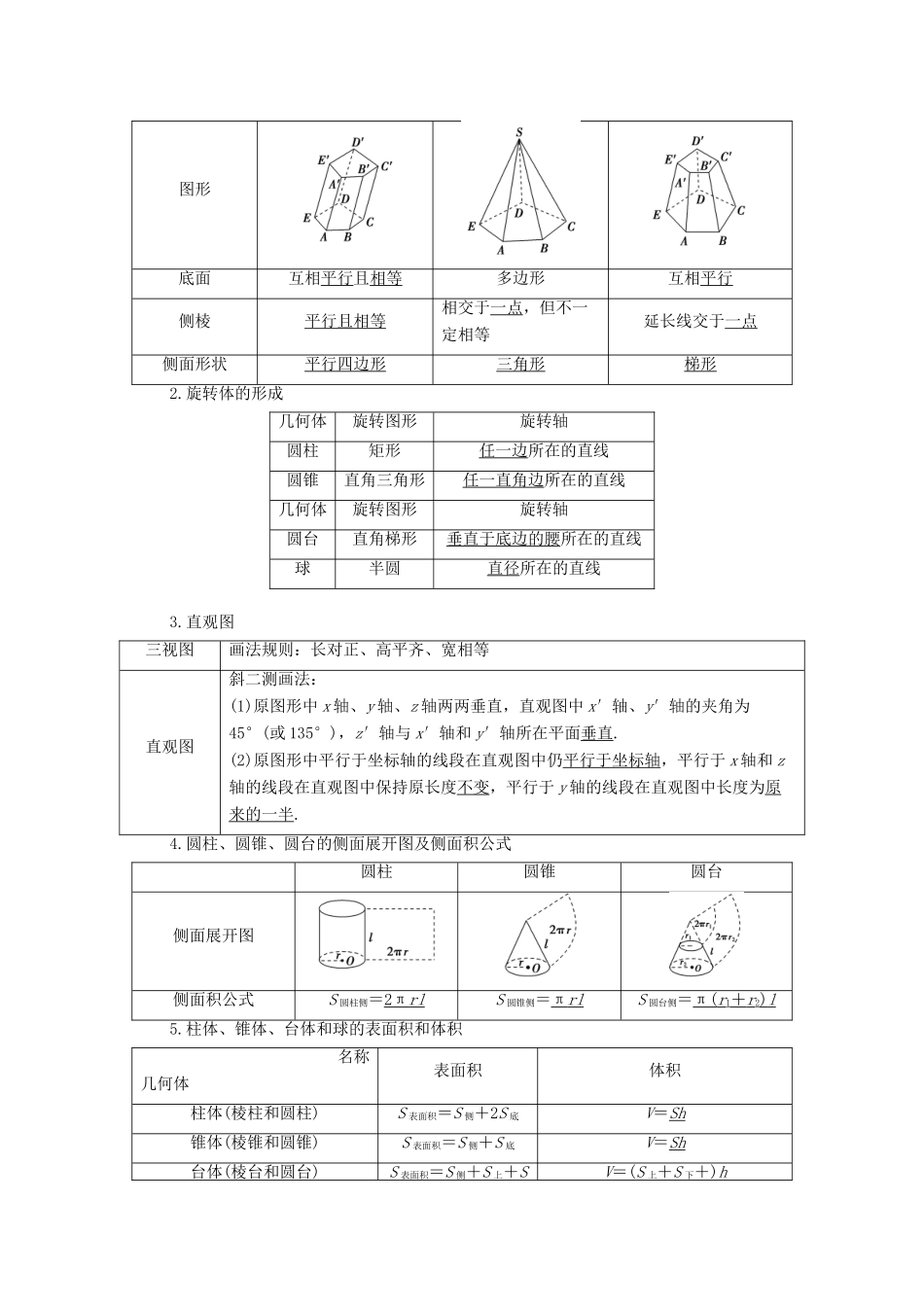
第七章 立体几何 全国卷五年考情图解高考命题规律把握1.考查形式高考在本章一般命制 2 道小题、1 道解答题,分值约占 22分.2.考查内容(1)小题主要考查几何体体积与表面积计算,此类问题属于中档题目;对于球与棱柱、棱锥的切接问题,知识点较整合,难度稍大.(2)解答题一般位于第 18 题或第19 题的位置,常设计两问:第(1)问重点考查线面位置关系的证明;第(2)问重点考查空间角,尤其是二面角、线面角的计算.属于中档题目.3.备考策略从 2019 年高考试题可以看出,高考对对空间几何体的展开、平面图形的折叠、解题中的补体等传统几何思想有所加强.第一节 空间几何体的结构及其表面积、体积[最新考纲] 1.认识柱、锥、台、球及其简单组合体的结构特征,并能够运用这些特征描述现实生活中简单物体的结构.2.会用斜二测画法画出常见几何体:长方体、球、圆柱、圆锥、棱柱等的直观图.3.了解球、棱柱、棱锥、棱台、圆柱、圆锥、圆台的表面积与体积的计算公式.1.多面体的结构特征名称棱柱棱锥棱台图形底面互相平行且相等多边形互相平行侧棱平行且相等相交于一点,但不一定相等延长线交于一点侧面形状平行四边形三角形梯形2.旋转体的形成几何体旋转图形旋转轴圆柱矩形任一边所在的直线圆锥直角三角形任一直角边所在的直线几何体旋转图形旋转轴圆台直角梯形垂直于底边的腰所在的直线球半圆直径所在的直线3.直观图三视图画法规则:长对正、高平齐、宽相等直观图斜二测画法:(1)原图形中 x 轴、y 轴、z 轴两两垂直,直观图中 x′轴、y′轴的夹角为45°(或 135°),z′轴与 x′轴和 y′轴所在平面垂直.(2)原图形中平行于坐标轴的线段在直观图中仍平行于坐标轴,平行于 x 轴和 z轴的线段在直观图中保持原长度不变,平行于 y 轴的线段在直观图中长度为原来的一半.4.圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱圆锥圆台侧面展开图侧面积公式S 圆柱侧=2π rl S 圆锥侧=π rl S 圆台侧=π( r 1+ r 2) l 5.柱体、锥体、台体和球的表面积和体积 名称几何体 表面积体积柱体(棱柱和圆柱)S 表面积=S 侧+2S 底V=Sh锥体(棱锥和圆锥)S 表面积=S 侧+S 底V=Sh台体(棱台和圆台)S 表面积=S 侧+S 上+SV=(S 上+S 下+)h下球S=4π R 2 V=πR3[常用结论]1.按照斜二测画法得到的平面图形的直观图,其面积与原图形的面积的关系:S 直观图=S 原图形,S 原图形=2 S 直观图.2.多面体的内切球与外接...