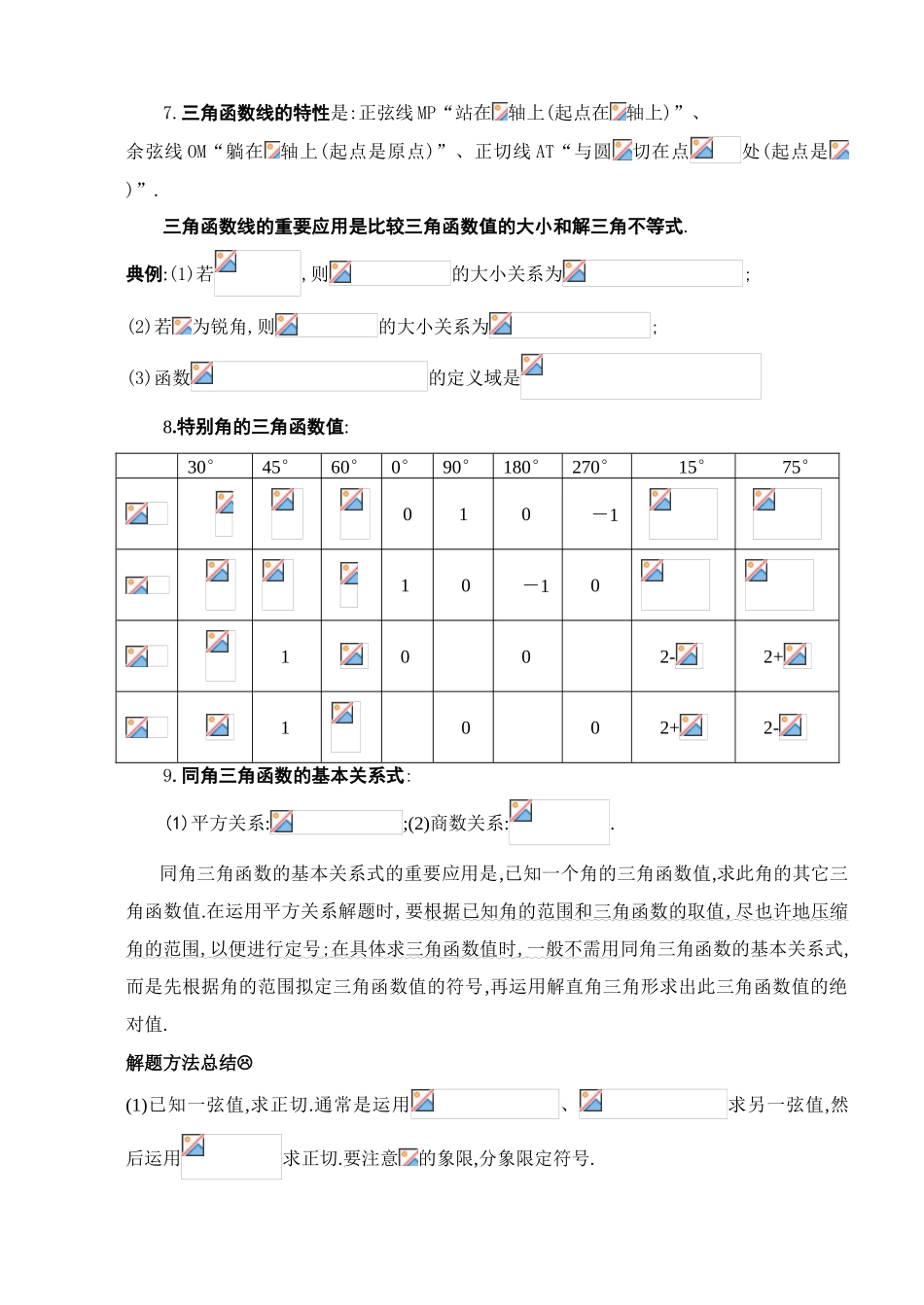
OR1radR新课标——回归教材三角函数1.角的概念的推广:平面内一条射线绕着端点从一个位置旋转到另一个位置所的图形.按逆时针方向旋转所形成的角叫正角,按顺时针方向旋转所形成的角叫负角,一条射线没有作任何旋转时,称它形成一个零角.射线的起始位置称为始边,终止位置称为终边.2.象限角的概念:在直角坐标系中,使角的顶点与原点重合,角的始边与轴的非负半轴重合,角的终边在第几象限,就说这个角是第几象限的角.假如角的终边在坐标轴上,就认为这个角不属于任何象限.3. 弧度制:把长度等于半径长的弧所对的圆心角叫做 1 弧度的角.1(rad)=,(rad).弧长公式:,扇形面积公式:. 典例:已知扇形的周长是 6cm,该扇形的中心角是 1 弧度,求该扇形的面积.(答:2)4.终边相同的角的表达: (1)终边与终边相同(的终边在终边所在射线上),注意:相等的角的终边一定相同,终边相同的角不一定相等.典例:与角的终边相同,且绝对值最小的角的度数是,合弧度.(2)终边在坐标轴上的角可表达为:.典例:的终边与的终边关于直线对称,则=.(3)各种角的集合表达名称角度表达形式()弧度表达形式()第一象限角第二象限角第三象限角第四象限角xyTAMPO终边落在 x 轴上终边落在 y 轴上终边落在 y=x 轴上终边落在 y=-x 轴上推断一个角的终边在哪个象限?是第几象限角?是解决后面一系列问题的基础.那么我们是如何鉴定?通常是把一个绝对值很大的角化成, 或者是化成,这样只要鉴定是第几象限角就可以了.典例: (1),由于是第一象限角,所以的终边也在第一象限;(2) ,由于是第一象限角,所以的终边也在第一象限.5.与的终边关系:由“两等分各象限、一二三四”拟定.如图,若角终边在第一(二、三、四)象限,则角的终边位于右图中标有数字 1(2、3、4)区域.这个方法叫做等分象限法.典例:若是第二象限角,则是第 一、三 象限角.6.任意角的三角函数的定义:设是任意一个角,P是的终边上的任意一点(异于原 点 ), 它 与 原 点 的 距 离 是, 那 么,.三角函数值只与角的大小有关,而与终边上点 P 的位置无关.典例:(1)已知角的终边通过点 P(5,-12),则的值为;(2)设是第三、四象限角,,则的取值范围是;(3)若,试推断的符号(答:负)yx12341234y=xy= -x7.三角函数线的特性是:正弦线 MP“站在轴上(起点在轴上)”、余弦线 OM“躺在轴上(起点是原点)”、正切线 AT“与圆切在点处(起点是)”.三角函数线的重要应用是比较三角函数值的大小和解三角不等式.典例:(1)若,则的大小关系为;(2)若为锐角...