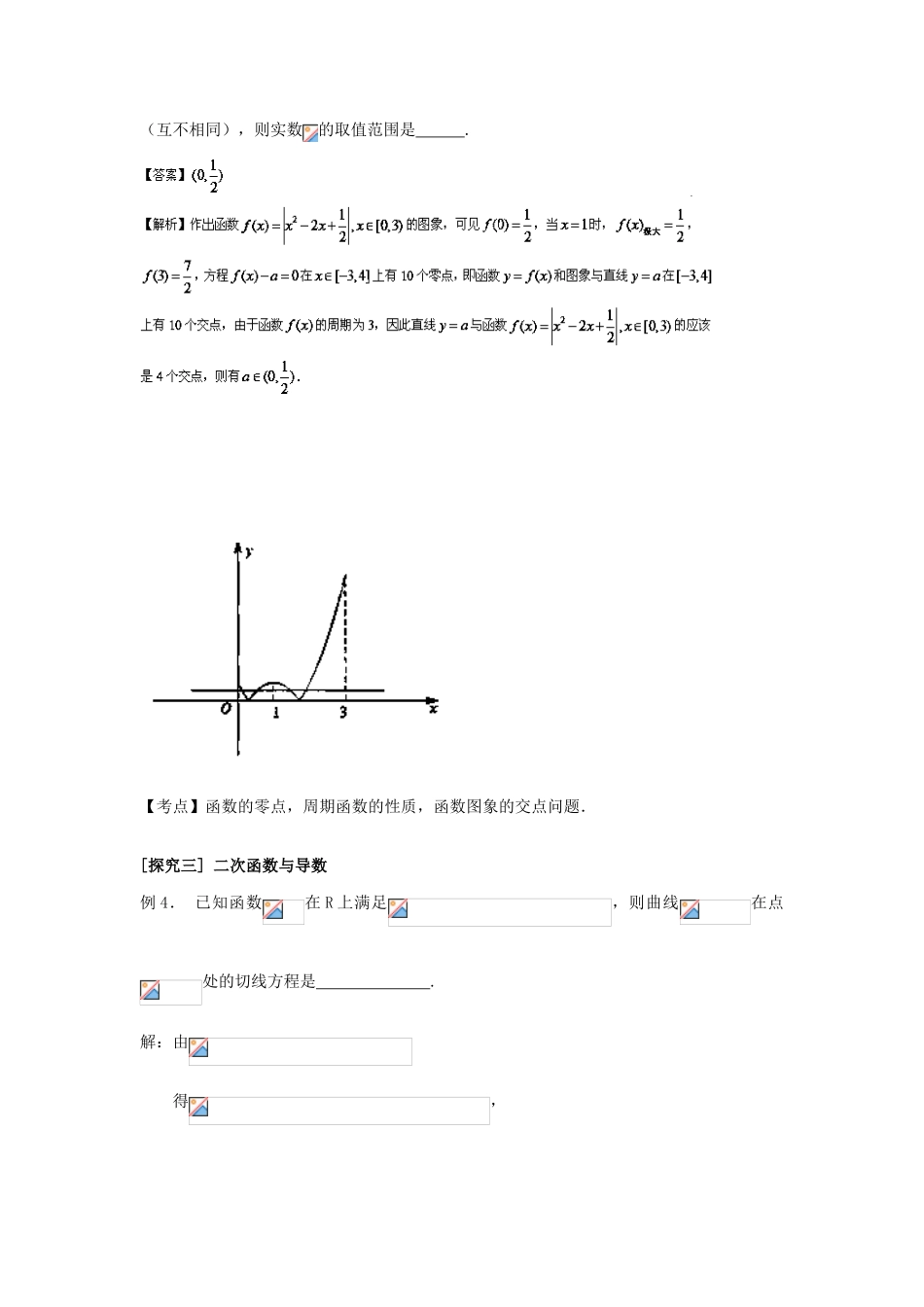
课题:二次函数(1)一、知识梳理二次函数作为最基本的初等函数,可以以它为素材来研究函数的解析式、定义域、值域、单调性、奇偶性等性质,还可建立起函数、方程、不等式之间的有机联系;二次函数可以编制出层出不穷、灵活多变的数学问题. 二次函数研究就应从两个方面入手:一是解析式,二是图像特征.从解析式出发,可以进行纯粹的代数推理,这种代数推理、论证的能力反映出一个人的基本数学素养;从图像特征出发,可以实现数与形的自然结合,这正是中学数学中一种非常重要的思想方法.1、二次函数解析式的三种形式一般式:顶点式:零点式:存在零点,则有2、二次函数的图象和性质 (1)、二次函数的图象是一条抛物线,抛物线 的对称轴是 ,顶点的坐标 ,因此对任意的实数 x,都有 。当 时,抛物线开中方向 ,在区间 上是递增,在区间 上 ,是递减,因此抛物线在 处,取得最小值 。当 时,抛物线开中方向 ,在区间 上是递增,在区间 上 ,是递减,因此抛物线在 处,取得最大值 。(2)、二次函数的图象与 x 轴的位置关系:由判别式判定3、二次函数,二次方程,二次不等式的关系一般地,设二次函数,二次方程的根的差别式 ,我们可以利用二次方程的根求出不等式,或,解集,它们的关系如下表:二次函数()的图象二次方程的根==没有实数根()的解集(-)R()的解集(,)二、题型探究[探究一]二次函数的最值问题例 1:已知函数 f(x)=,t 为实数,求函数的最小值。变式:如何求函数的最大值。[探究二] 二次函数与一元二次方程例 2.若函数是偶函数,则函数的最小值为 .解:∵二次函数是偶函数,∴其图像关于轴对称.∴.∴函数的最小值为.例 3:【2014 高考江苏卷第 13 题】已知是定义在上且周期为 3 的函数,当时,,若函数在区间上有 10 个零点(互不相同),则实数的取值范围是 .【考点】函数的零点,周期函数的性质,函数图象的交点问题.[探究三] 二次函数与导数例 4. 已知函数在 R 上满足,则曲线在点处的切线方程是 .解:由得,即,∴∴,∴切线方程为,即例 5.设函数,曲线在点处的切线方程为,则曲线在点处切线的斜率为 .解:由已知,而,∴[探究四] 二次函数与恒成立问题例 6.若函数的定义域为一切实数,则实数的取值范围是 .解:由已知对一切实数恒成立.(1)当时,满足题意;(2)当时,只须解得.由(1)、(2)得.练习:若函数的定义域为一切实数,则实数的取值范围是 .解:由已知对一切实数恒成立.(1)当时,满足题意;(2)当时,只须.解得.由(1)、(2)得.