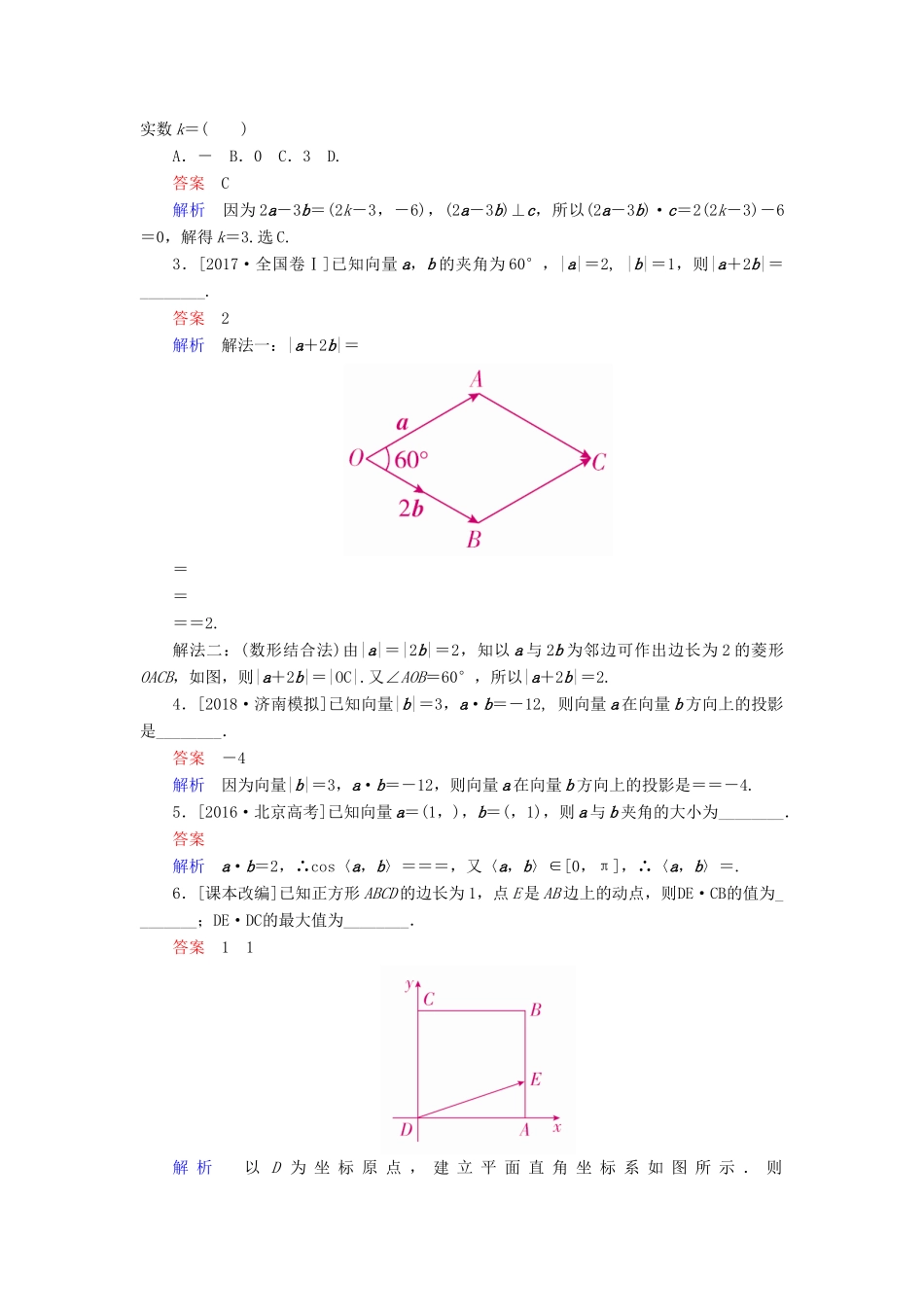
第 3 讲 平面向量的数量积及应用板块一 知识梳理·自主学习[必备知识]考点 1 数量积的有关概念1.两个非零向量 a 与 b,过 O 点作OA=a,OB=b,则∠ AOB = θ ,叫做向量 a 与 b 的夹角;范围是 0°≤θ≤180°.2.a 与 b 的夹角为 90 度时,叫 a⊥b.3.若 a 与 b 的夹角为 θ,则 a·b=|a||b|cosθ.4.若 a=(x1,y1),b=(x2,y2),则 a·b=x1x2+ y 1y2.5.a 在 b 的方向上的投影为|a|cosθ.6.若 a=(x1,y1),b=(x2,y2),夹角为 θ,则|a|=,cosθ=.a⊥b⇔x1x2+ y 1y2= 0 .a∥b⇔x1y2- x 2y1= 0 .考点 2 数量积满足的运算律已知向量 a,b,c 和实数 λ,则向量的数量积满足下列运算律:1.a·b=b·a.2.(λa)·b=λ(a·b)=a·(λb).3.(a+b)·c=a·c+b·c.[必会结论]1.设 e 是单位向量,且 e 与 a 的夹角为 θ,则 e·a=a·e=|a|cosθ;2.当 a 与 b 同向时,a·b=|a||b|;当 a 与 b 反向时,a·b=-|a||b|,特别地,a·a=a2或|a|=;3.a·b≤|a||b|.[考点自测]1.判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)两个向量的数量积是一个向量.( )(2)向量在另一个向量方向上的投影也是向量.( )(3)若 a·b>0,则 a 和 b 的夹角为锐角;若 a·b<0,则 a 和 b 的夹角为钝角.( )(4)若 a·b=0,则 a=0 或 b=0.( )(5)(a·b)·c=a·(b·c).( )(6)若 a·b=a·c(a≠0),则 b=c.( )答案 (1)× (2)× (3)× (4)× (5)× (6)×2.[2018·重庆模拟]已知向量 a=(k,3),b=(1,4),c=(2,1),且(2a-3b)⊥c,则实数 k=( )A.- B.0 C.3 D.答案 C解析 因为 2a-3b=(2k-3,-6),(2a-3b)⊥c,所以(2a-3b)·c=2(2k-3)-6=0,解得 k=3.选 C.3.[2017·全国卷Ⅰ]已知向量 a,b 的夹角为 60°,|a|=2, |b|=1,则|a+2b|=________.答案 2解析 解法一:|a+2b|=====2.解法二:(数形结合法)由|a|=|2b|=2,知以 a 与 2b 为邻边可作出边长为 2 的菱形OACB,如图,则|a+2b|=|OC|.又∠AOB=60°,所以|a+2b|=2.4.[2018·济南模拟]已知向量|b|=3,a·b=-12, 则向量 a 在向量 b 方向上的投影是________.答案 -4解析 因为向量|b|=3,a·b=-12,则向量 a 在向量 b 方向上的投影是==-4.5.[2016·北京高考]已知向量 a=(1,),b=(,1),则 a ...