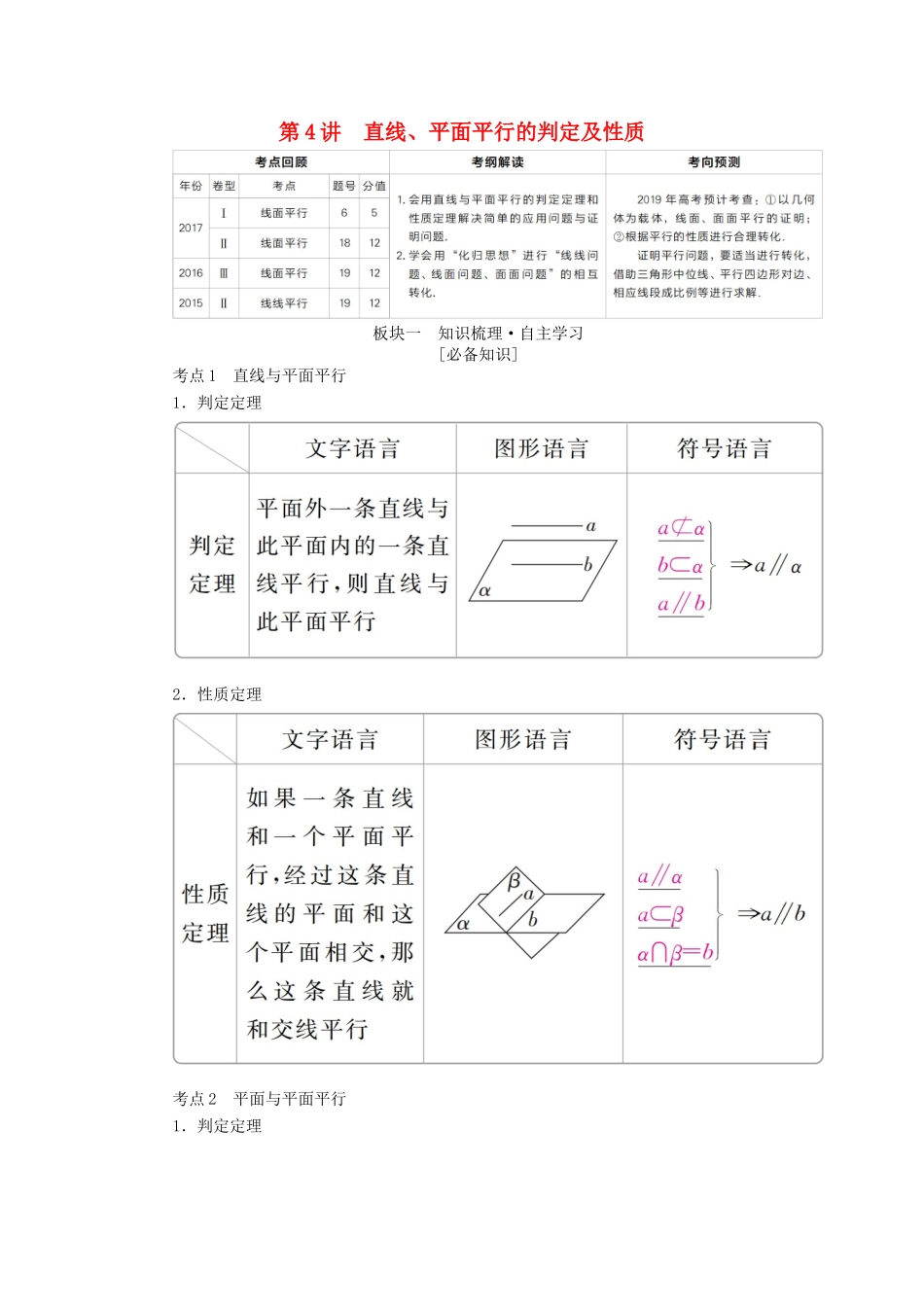
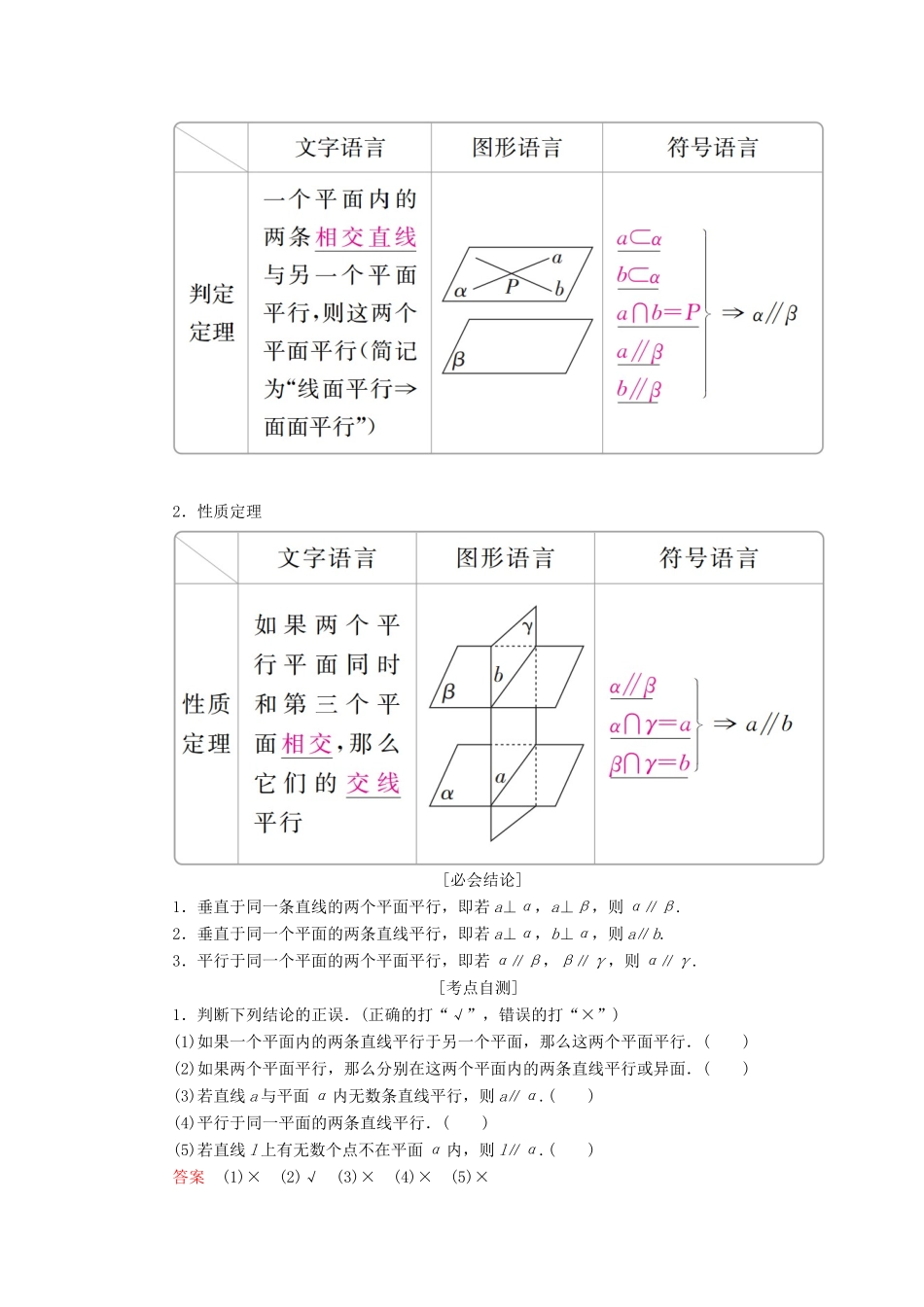
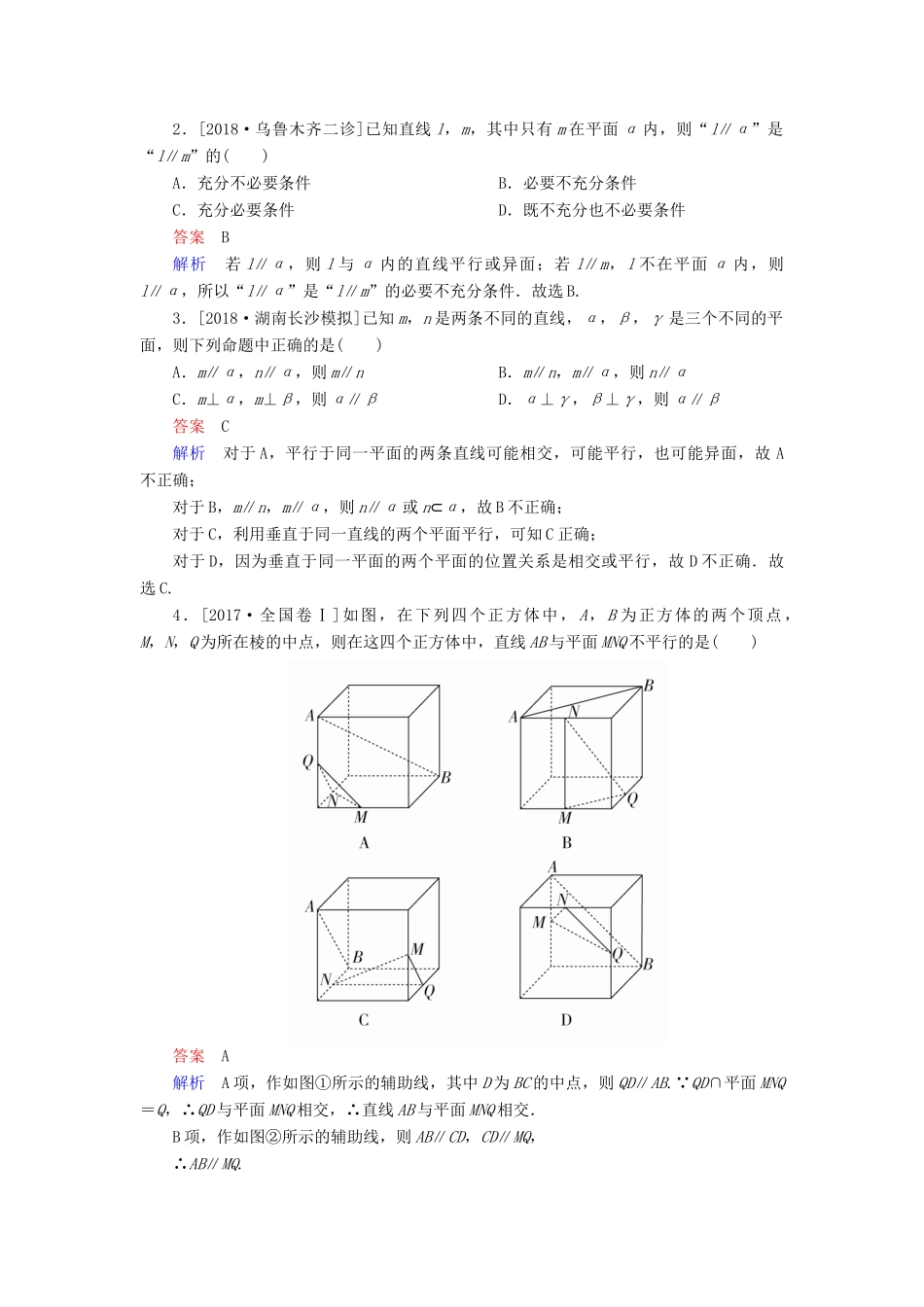
第 4 讲 直线、平面平行的判定及性质板块一 知识梳理·自主学习[必备知识]考点 1 直线与平面平行1.判定定理2.性质定理考点 2 平面与平面平行1.判定定理2.性质定理 [必会结论]1.垂直于同一条直线的两个平面平行,即若 a⊥α,a⊥β,则 α∥β.2.垂直于同一个平面的两条直线平行,即若 a⊥α,b⊥α,则 a∥b.3.平行于同一个平面的两个平面平行,即若 α∥β,β∥γ,则 α∥γ.[考点自测] 1.判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)如果一个平面内的两条直线平行于另一个平面,那么这两个平面平行.( )(2)如果两个平面平行,那么分别在这两个平面内的两条直线平行或异面.( )(3)若直线 a 与平面 α 内无数条直线平行,则 a∥α.( )(4)平行于同一平面的两条直线平行.( )(5)若直线 l 上有无数个点不在平面 α 内,则 l∥α.( )答案 (1)× (2)√ (3)× (4)× (5)×2.[2018·乌鲁木齐二诊]已知直线 l,m,其中只有 m 在平面 α 内,则“l∥α”是“l∥m”的( )A.充分不必要条件 B.必要不充分条件C.充分必要条件 D.既不充分也不必要条件答案 B解析 若 l∥α,则 l 与 α 内的直线平行或异面;若 l∥m,l 不在平面 α 内,则l∥α,所以“l∥α”是“l∥m”的必要不充分条件.故选 B.3.[2018·湖南长沙模拟]已知 m,n 是两条不同的直线,α,β,γ 是三个不同的平面,则下列命题中正确的是( )A.m∥α,n∥α,则 m∥n B.m∥n,m∥α,则 n∥αC.m⊥α,m⊥β,则 α∥β D.α⊥γ,β⊥γ,则 α∥β答案 C解析 对于 A,平行于同一平面的两条直线可能相交,可能平行,也可能异面,故 A不正确;对于 B,m∥n,m∥α,则 n∥α 或 n⊂α,故 B 不正确;对于 C,利用垂直于同一直线的两个平面平行,可知 C 正确;对于 D,因为垂直于同一平面的两个平面的位置关系是相交或平行,故 D 不正确.故选 C.4.[2017·全国卷Ⅰ]如图,在下列四个正方体中, A,B 为正方体的两个顶点,M,N,Q 为所在棱的中点,则在这四个正方体中,直线 AB 与平面 MNQ 不平行的是( )答案 A解析 A 项,作如图①所示的辅助线,其中 D 为 BC 的中点,则 QD∥AB. QD∩平面 MNQ=Q,∴QD 与平面 MNQ 相交,∴直线 AB 与平面 MNQ 相交.B 项,作如图②所示的辅助线,则 AB∥CD,CD∥MQ,∴AB∥MQ.又 AB⊄平面 MNQ,MQ⊂平面 MNQ...