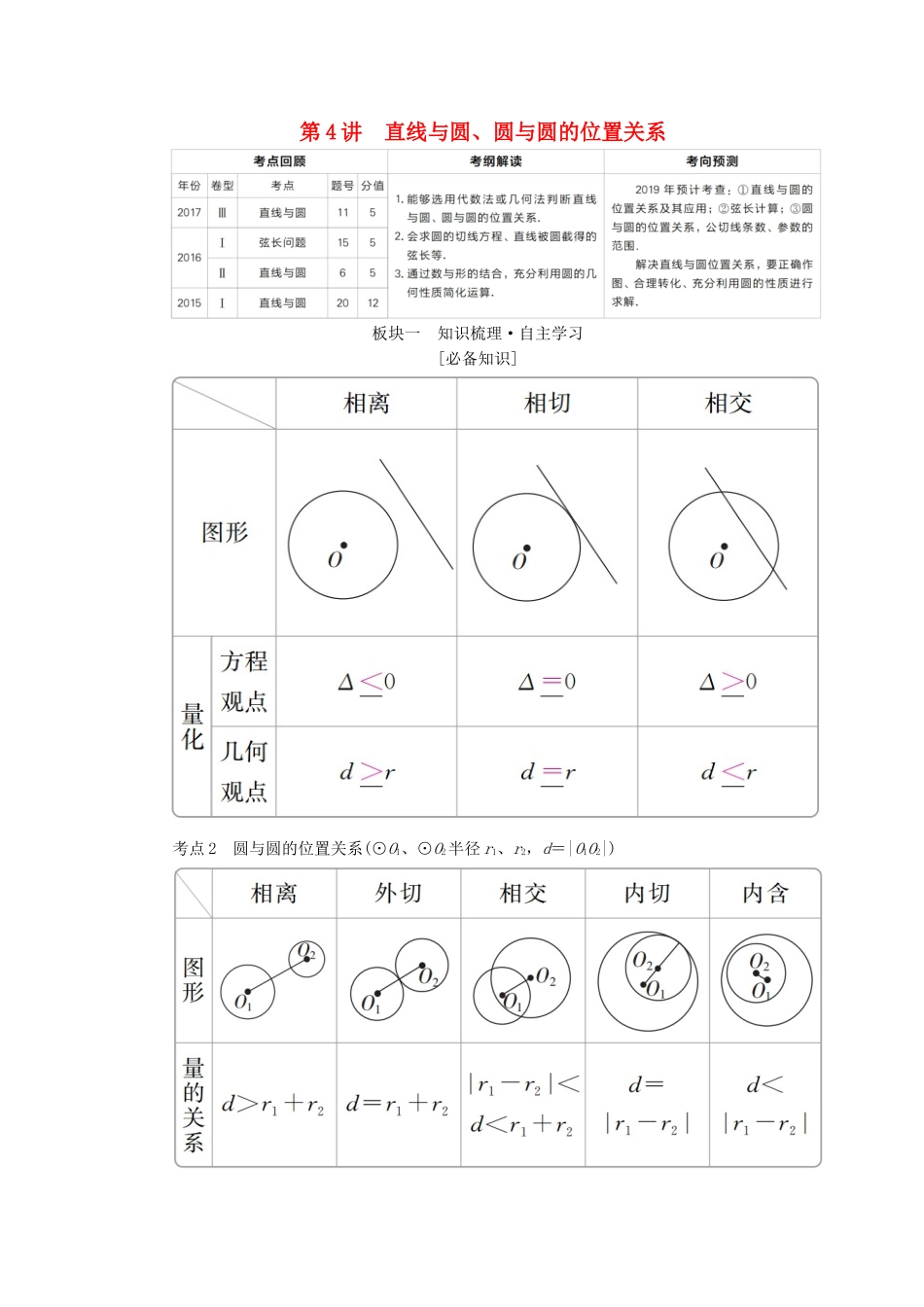
第 4 讲 直线与圆、圆与圆的位置关系板块一 知识梳理·自主学习[必备知识]考点 2 圆与圆的位置关系(⊙O1、⊙O2半径 r1、r2,d=|O1O2|)[必会结论]1.关注一个直角三角形当直线与圆相交时,由弦心距(圆心到直线的距离)、弦长的一半及半径构成一个直角三角形.2.圆心在过切点且垂直于切线的直线上.3.两圆相交时公共弦的方程设圆 C1:x2+y2+D1x+E1y+F1=0,①圆 C2:x2+y2+D2x+E2y+F2=0,②若两圆相交,则有一条公共弦,其公共弦所在直线方程由①-②所得,即:(D1-D2)x+(E1-E2)y+(F1-F2)=0.4.两圆相切时,切点与两圆心三点共线.5.两圆不同的位置关系与对应公切线的条数(1)两圆外离时,有 4 条公切线;(2)两圆外切时,有 3 条公切线;(3)两圆相交时,有 2 条公切线;(4)两圆内切时,有 1 条公切线;(5)两圆内含时,没有公切线. [考点自测]1.判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)“k=1”是“直线 x-y+k=0 与圆 x2+y2=1 相交”的必要不充分条件.( )(2)过圆 O:x2+y2=r2上一点 P(x0,y0)的圆的切线方程是 x0x+y0y=r2.( )(3)如果两个圆的方程组成的方程组只有一组实数解,则两圆外切.( )(4)如果两圆的圆心距小于两圆的半径之和,则两圆相交.( )(5)“m=0”是“直线 x+y-m=0 与圆(x-1)2+(y-1)2=2 相切”的充分不必要条件.( )答案 (1)× (2)√ (3)× (4)× (5)√2.[课本改编]直线 l:x-y+1=0 与圆 C:x2+y2-4x-2y+1=0 的位置关系是( )A.相离 B.相切C.相交且过圆心 D.相交但不过圆心答案 D解析 圆的方程化为(x-2)2+(y-1)2=4,圆心为(2,1),半径为 2,圆心到直线 l 的距离为=<2,所以直线 l 与圆相交.又圆心不在直线 l 上,所以直线不过圆心.故选 D.3.在平面直角坐标系 xOy 中,直线 3x+4y-5=0 与圆 x2+y2=4 相交于 A,B 两点,则弦 AB 的长为( )A.3 B.2 C. D.1答案 B解析 圆心(0,0)到直线 3x+4y-5=0 的距离 d==1,因为 2=22-12=3,所以|AB|=2.4.[课本改编]圆 x2+y2-4x=0 在点 P(1,)处的切线方程为( )A.x+y-2=0 B.x+y-4=0C.x-y+4=0 D.x-y+2=0答案 D解析 圆的方程为(x-2)2+y2=4,圆心坐标为(2,0),半径为 2,点 P 在圆上,由题可知切线的斜率存在,设切线方程为 y-=k(x-1),即 kx-y-k+=0,∴=2,解得 k=.∴切线方程为 y...