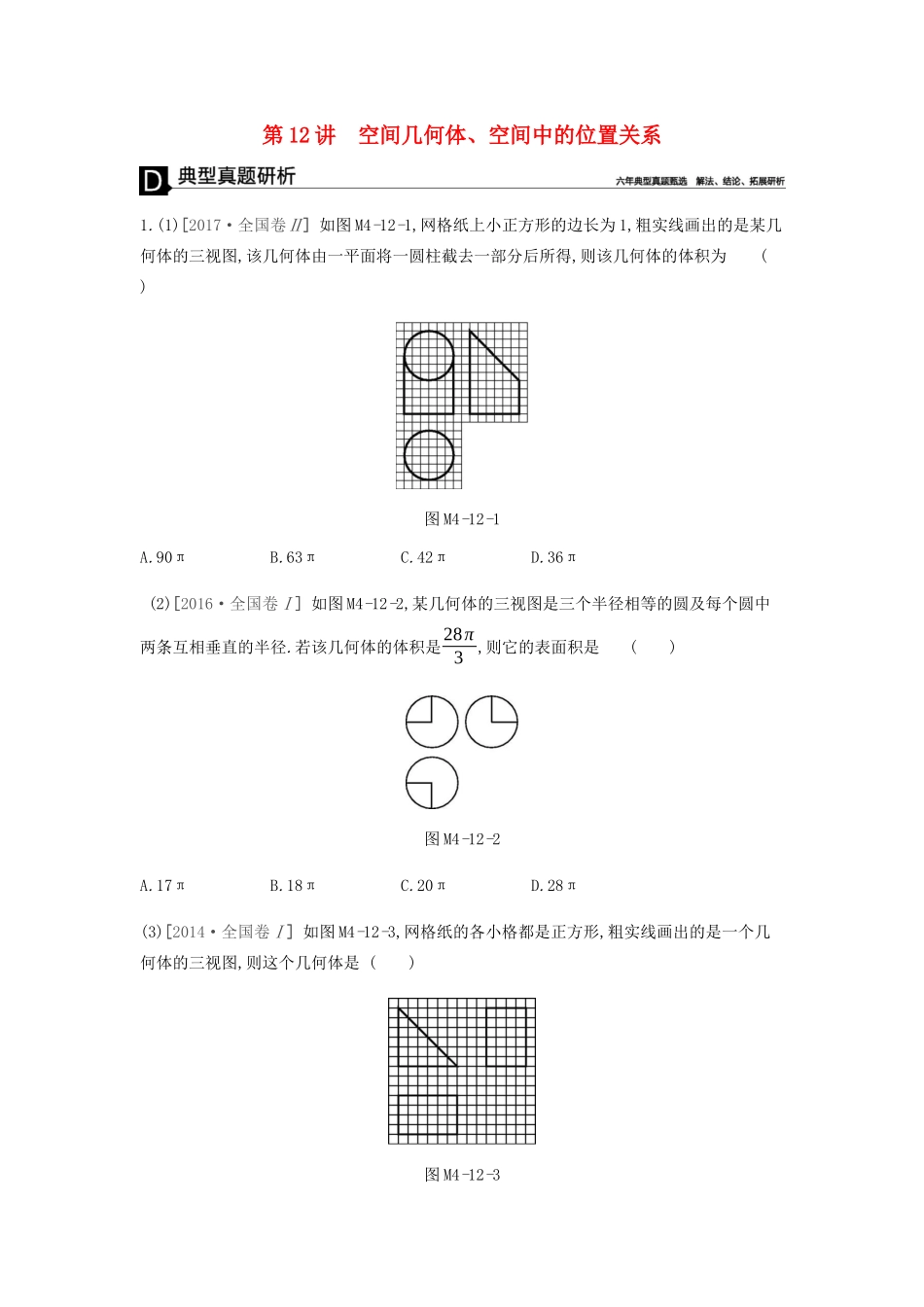
第 12 讲 空间几何体、空间中的位置关系1.(1)[2017·全国卷Ⅱ] 如图 M4-12-1,网格纸上小正方形的边长为 1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )图 M4-12-1A.90π B.63π C.42π D.36π (2)[2016·全国卷Ⅰ] 如图 M4-12-2,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是28π3,则它的表面积是( )图 M4-12-2A.17πB.18πC.20πD.28π(3)[2014·全国卷Ⅰ] 如图 M4-12-3,网格纸的各小格都是正方形,粗实线画出的是一个几何体的三视图,则这个几何体是 ( )图 M4-12-3A.三棱锥B.三棱柱C.四棱锥D.四棱柱(4)[2013·全国卷Ⅱ] 一个四面体的顶点在空间直角坐标系 O-xyz 中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以 zOx 平面为投影面,则得到的正视图可以为( )图 M4-12-4[试做] ______________________________________________________________________________________________________________________________________________________命题角度 三视图问题(1)根据三视图求几何体体积的解题策略:关键一:根据三视图确定几何体的结构特征,作出其直观图,由三视图中的数据确定几何体的数字特征;关键二:根据组合体的结构特征,利用分割法、补形法将其转化为规则的几何体,再求解.(2)根据几何体的三视图求表面积的解题策略:关键一:根据三视图确定几何体的结构特征,作出其直观图,由三视图中的数据确定几何体的数字特征;关键二:求组合体的表面积时,需注意组合体的衔接部分的面积;关键三:要分清侧面积和表面积.(3)由几何体的三视图还原几何体的形状的解题策略:关键一:熟悉柱、锥、台、球的三视图;关键二:明确三视图的形成原理,遵循“长对正、高平齐、宽相等”的原则,并结合空间想象将三视图还原为直观图.(4)由几何体的直观图求三视图的解题策略:关键一:注意正视图、侧视图和俯视图的观察方向;关键二:注意看到的部分是实线,看不到的部分是虚线.2.(1)[2014·全国卷Ⅱ] 正三棱柱 ABC-A1B1C1的底面边长为 2,侧棱长为❑√3,D 为 BC 中点,则三棱锥 A-B1DC1的体积为( )A.3B.32C.1D.❑√32命题角度 求三棱锥的体积对于三棱锥常用等体积转化法求体积:关键一:三棱锥的每个面都可以作为底面,寻找满足公式的底面和高;关键二:利用三棱锥体积公式求解.(2)[2015·全国卷Ⅰ] 《九章算术》是我国古代内容极...