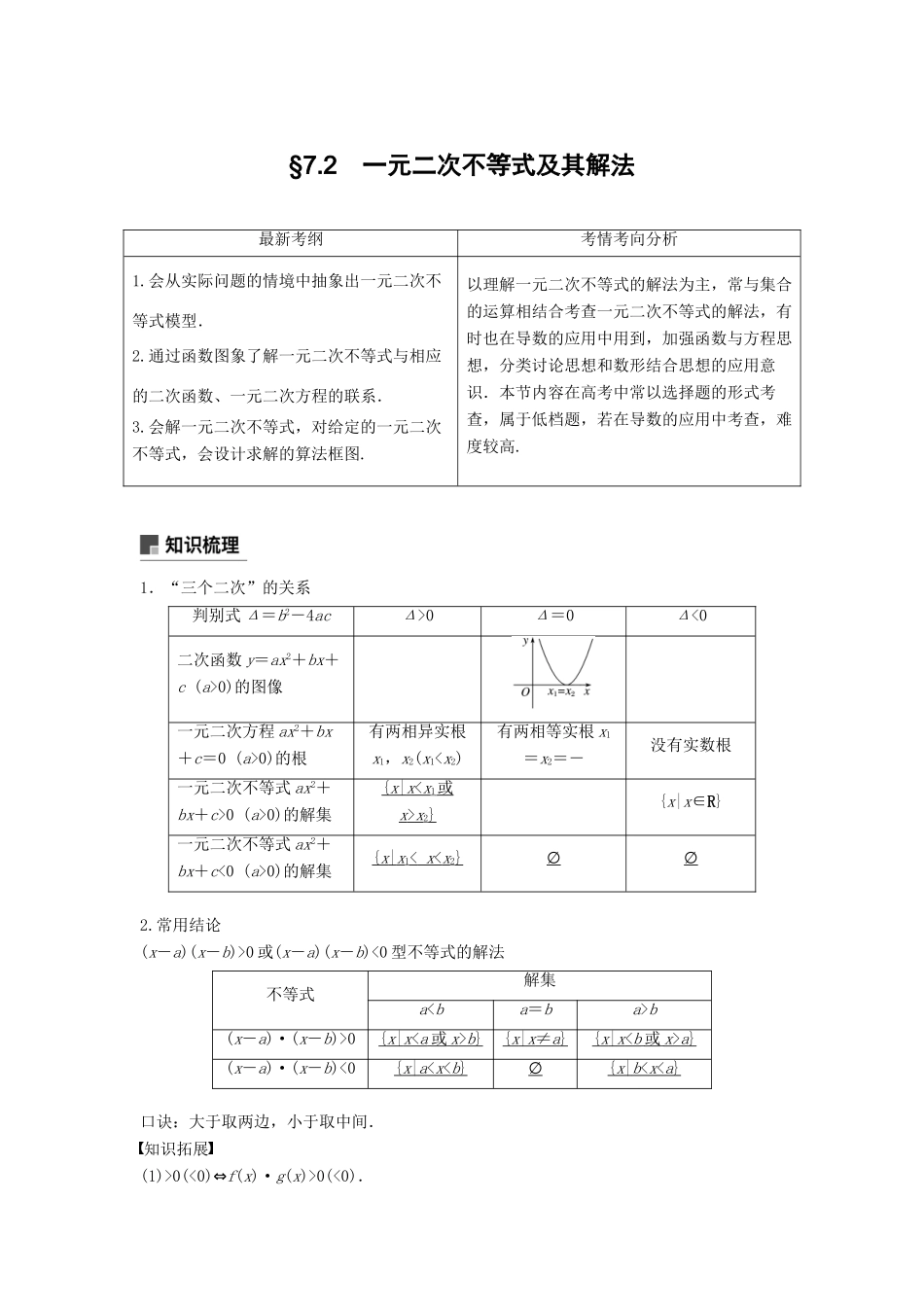
§7.2 一元二次不等式及其解法最新考纲考情考向分析1.会从实际问题的情境中抽象出一元二次不等式模型.2.通过函数图象了解一元二次不等式与相应的二次函数、一元二次方程的联系.3.会解一元二次不等式,对给定的一元二次不等式,会设计求解的算法框图.以理解一元二次不等式的解法为主,常与集合的运算相结合考查一元二次不等式的解法,有时也在导数的应用中用到,加强函数与方程思想,分类讨论思想和数形结合思想的应用意识.本节内容在高考中常以选择题的形式考查,属于低档题,若在导数的应用中考查,难度较高.1.“三个二次”的关系判别式 Δ=b2-4acΔ>0Δ=0Δ<0二次函数 y=ax2+bx+c (a>0)的图像一元二次方程 ax2+bx+c=0 (a>0)的根有两相异实根x1,x2(x10 (a>0)的解集{ x | x < x 1 或x > x 2}{x|x∈R}一元二次不等式 ax2+bx+c<0 (a>0)的解集{ x | x 1< x < x 2}∅∅2.常用结论(x-a)(x-b)>0 或(x-a)(x-b)<0 型不等式的解法不等式解集ab(x-a)·(x-b)>0{ x | x < a 或 x > b } { x | x ≠ a } { x | x < b 或 x > a } (x-a)·(x-b)<0{ x | a < x < b } ∅{ x | b < x < a } 口诀:大于取两边,小于取中间.知识拓展(1)>0(<0)⇔f(x)·g(x)>0(<0).(2)≥0(≤0)⇔f(x)·g(x)≥0(≤0)且 g(x)≠0.以上两式的核心要义是将分式不等式转化为整式不等式.题组一 思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)若不等式 ax2+bx+c<0 的解集为(x1,x2),则必有 a>0.( √ )(2)若不等式 ax2+bx+c>0 的解集是(-∞,x1)∪(x2,+∞),则方程 ax2+bx+c=0 的两个根是 x1和 x2.( √ )(3)若方程 ax2+bx+c=0(a≠0)没有实数根,则不等式 ax2+bx+c>0 的解集为 R.( × )(4)不等式 ax2+bx+c≤0 在 R 上恒成立的条件是 a<0 且 Δ=b2-4ac≤0.( × )(5)若二次函数 y=ax2+bx+c 的图像开口向下,则不等式 ax2+bx+c<0 的解集一定不是空集.( √ )题组二 教材改编2.已知全集 U=R,集合 A={x|x2-x-6≤0},B=,那么集合 A∩(∁UB)等于( )A.[-2,4) B.(-1,3]C.[-2,-1] D.[-1,3]答案 D解析 因为 A={x|-2≤x≤3},B={x|x<-1 或 x≥4},故∁UB={x|-1≤x<4},所以 A∩(∁UB)={x|-1≤x≤3}...