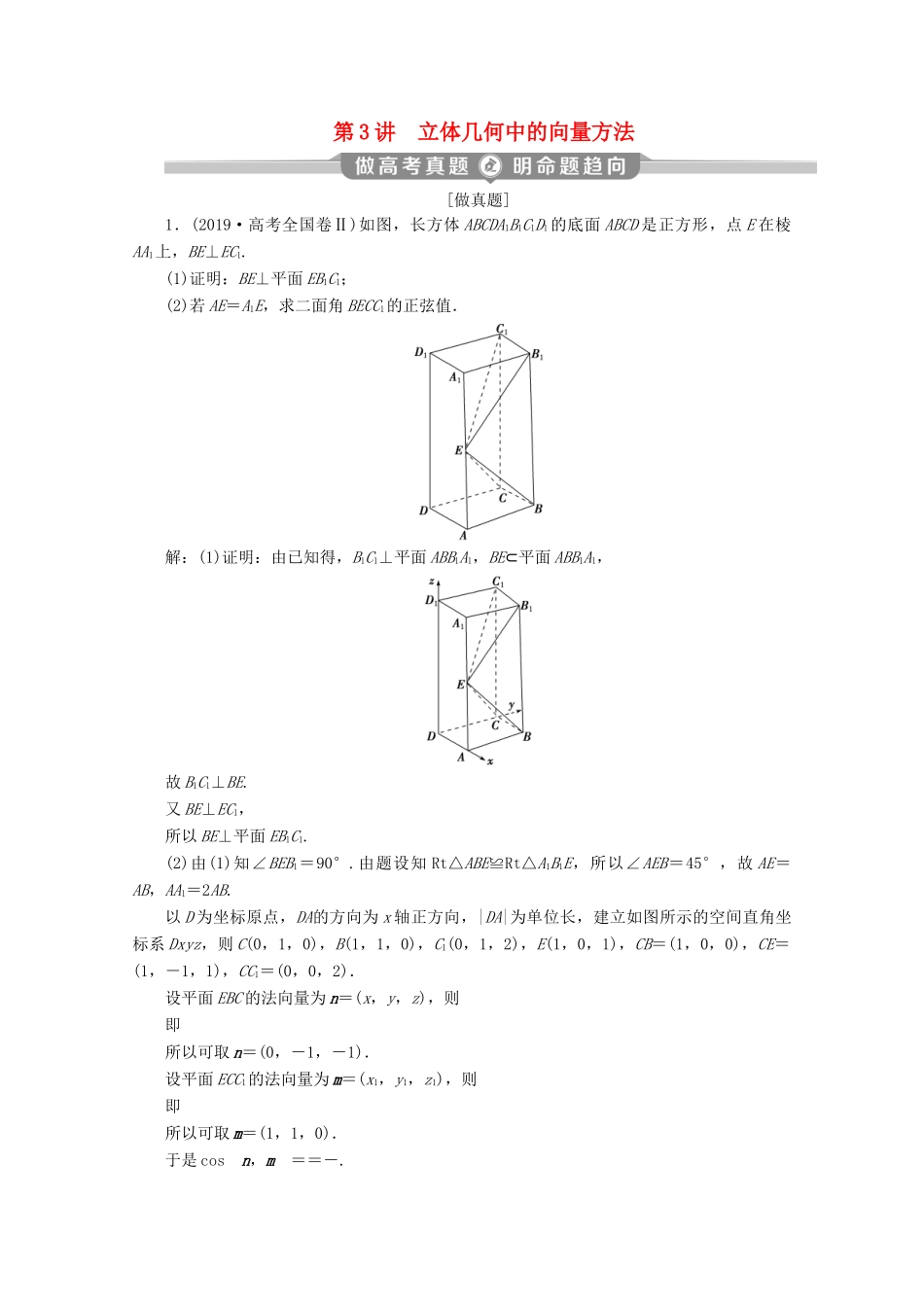
第 3 讲 立体几何中的向量方法[做真题]1.(2019·高考全国卷Ⅱ)如图,长方体 ABCDA1B1C1D1 的底面 ABCD 是正方形,点 E 在棱AA1上,BE⊥EC1.(1)证明:BE⊥平面 EB1C1;(2)若 AE=A1E,求二面角 BECC1的正弦值.解:(1)证明:由已知得,B1C1⊥平面 ABB1A1,BE⊂平面 ABB1A1,故 B1C1⊥BE.又 BE⊥EC1,所以 BE⊥平面 EB1C1.(2)由(1)知∠BEB1=90°.由题设知 Rt△ABE≌Rt△A1B1E,所以∠AEB=45°,故 AE=AB,AA1=2AB.以 D 为坐标原点,DA的方向为 x 轴正方向,|DA|为单位长,建立如图所示的空间直角坐标系 Dxyz,则 C(0,1,0),B(1,1,0),C1(0,1,2),E(1,0,1),CB=(1,0,0),CE=(1,-1,1),CC1=(0,0,2).设平面 EBC 的法向量为 n=(x,y,z),则即所以可取 n=(0,-1,-1).设平面 ECC1的法向量为 m=(x1,y1,z1),则即所以可取 m=(1,1,0).于是 cosn,m==-.所以,二面角 BECC1的正弦值为.2.(2018·高考全国卷Ⅰ)如图,四边形 ABCD 为正方形,E,F 分别为 AD,BC 的中点,以 DF 为折痕把△DFC 折起,使点 C 到达点 P 的位置,且 PF⊥BF.(1)证明:平面 PEF⊥平面 ABFD;(2)求 DP 与平面 ABFD 所成角的正弦值.解:(1)证明:由已知可得,BF⊥PF,BF⊥EF,所以 BF⊥平面 PEF.又 BF⊂平面 ABFD,所以平面 PEF⊥平面 ABFD.(2)作 PH⊥EF,垂足为 H.由(1)得,PH⊥平面 ABFD.以 H 为坐标原点,HF的方向为 y 轴正方向,|BF|为单位长,建立如图所示的空间直角坐标系 H-xyz.由(1)可得,DE⊥PE.又 DP=2,DE=1,所以 PE=.又 PF=1,EF=2,故 PE⊥PF.可得 PH=,EH=.则 H(0,0,0),P,D,DP=,HP=为平面 ABFD 的法向量.设 DP 与平面 ABFD 所成角为 θ,则 sin θ===.所以 DP 与平面 ABFD 所成角的正弦值为.[明考情]高考对此部分的命题较为稳定,一般为解答题,多出现在第 18 或 19 题的第二问的位置,考查利用空间向量求异面直线所成的角、线面角或二面角,难度中等偏上.利用空间向量证明平行与垂直[典型例题] 如图,在四棱锥 PABCD 中,PA⊥底面 ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点 E 为棱 PC 的中点.证明:(1)BE⊥DC;(2)BE∥平面 PAD;(3)平面 PCD⊥平面 PAD.【 证 明 】 依 题 意 , 以 点 A 为 原 点 建 立 空 间 直 角 坐 标 系 ( 如 图 ) , 可 得B(1 ,...