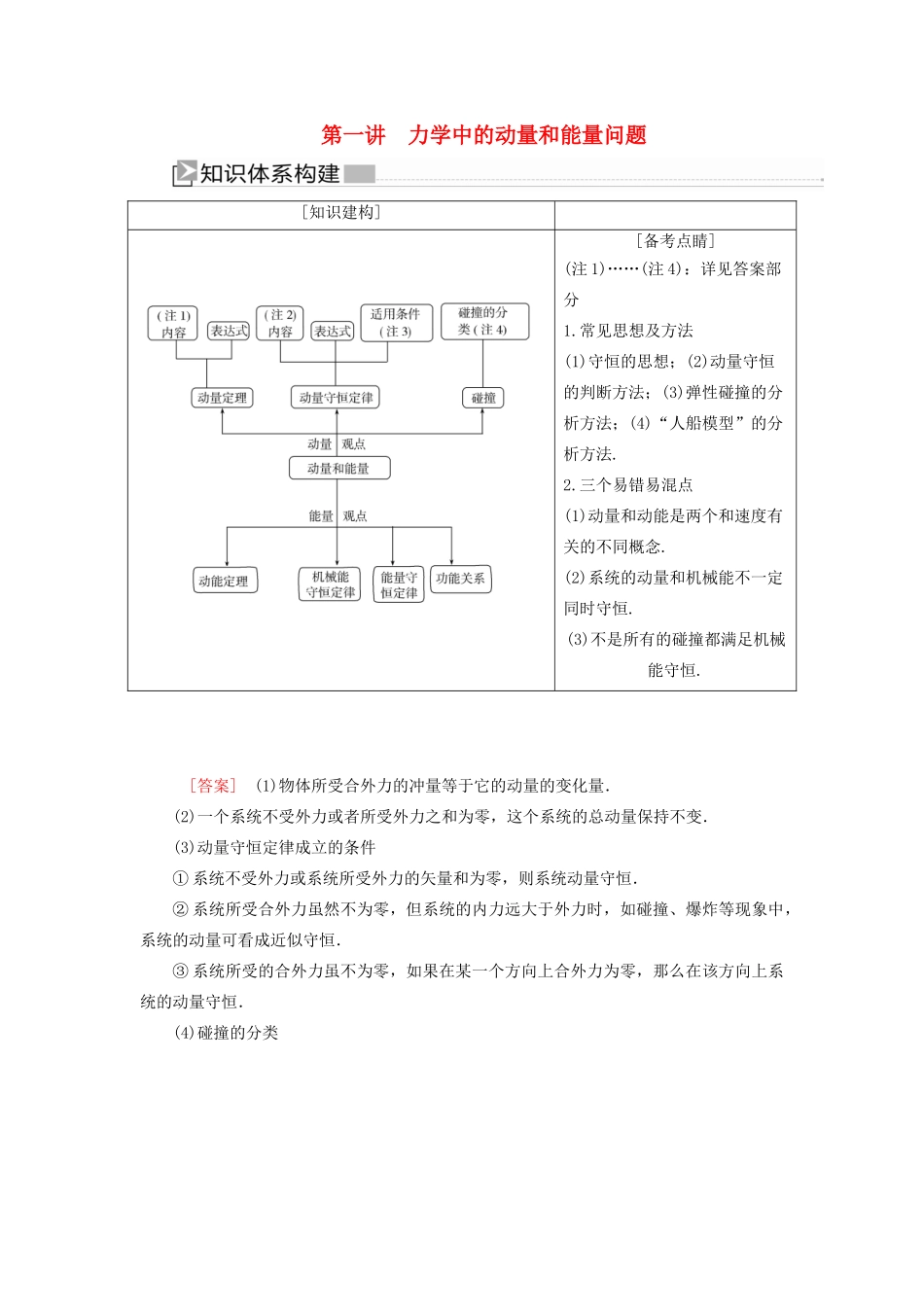
第一讲 力学中的动量和能量问题[知识建构][备考点睛](注 1)……(注 4):详见答案部分1.常见思想及方法(1)守恒的思想;(2)动量守恒的判断方法;(3)弹性碰撞的分析方法;(4)“人船模型”的分析方法.2.三个易错易混点(1)动量和动能是两个和速度有关的不同概念.(2)系统的动量和机械能不一定同时守恒.(3)不是所有的碰撞都满足机械能守恒. [答案] (1)物体所受合外力的冲量等于它的动量的变化量.(2)一个系统不受外力或者所受外力之和为零,这个系统的总动量保持不变.(3)动量守恒定律成立的条件① 系统不受外力或系统所受外力的矢量和为零,则系统动量守恒.② 系统所受合外力虽然不为零,但系统的内力远大于外力时,如碰撞、爆炸等现象中,系统的动量可看成近似守恒.③ 系统所受的合外力虽不为零,如果在某一个方向上合外力为零,那么在该方向上系统的动量守恒.(4)碰撞的分类热点考向一 动量定理与动量守恒定律的应用角度一 动量定理的应用【典例 1】 (2016·全国卷Ⅰ)某游乐园入口旁有一喷泉,喷出的水柱将一质量为 M的卡通玩具稳定地悬停在空中.为计算方便起见,假设水柱从横截面积为 S 的喷口持续以速度 v0竖直向上喷出;玩具底部为平板(面积略大于 S);水柱冲击到玩具底板后,在竖直方向水的速度变为零,在水平方向朝四周均匀散开.忽略空气阻力.已知水的密度为 ρ,重力加速度大小为 g.求:(1)喷泉单位时间内喷出的水的质量;(2)玩具在空中悬停时,其底面相对于喷口的高度.[思路引领] [解析] (1)设 Δt 时间内,从喷口喷出的水的体积为 ΔV,质量为 Δm,则 Δm=ρΔV①ΔV=v0SΔt②由①②式得,单位时间内从喷口喷出的水的质量=ρv0S③(2)设玩具悬停时其底面相对于喷口的高度为 h,水从喷口喷出后到达玩具底面时的速度大小为 v.对于 Δt 时间内喷出的水,由能量守恒得(Δm)v2+(Δm)gh=(Δm)v④在 h 高度处,Δt 时间内喷射到玩具底面的水沿竖直方向的动量变化量的大小 Δp=(Δm)v⑤设水对玩具的作用力的大小为 F,根据动量定理有FΔt=Δp⑥由于玩具在空中悬停,由力的平衡条件得 F=Mg⑦联立③④⑤⑥⑦式得 h=-[答案] (1)ρv0S (2)-角度二 动量守恒定律的应用【典例 2】 (2018·全国卷Ⅰ)一质量为 m 的烟花弹获得动能 E 后,从地面竖直升空.当烟花弹上升的速度为零时,弹中火药爆炸将烟花弹炸为质量相等的两部分,两部分获得的动能之和也为 E,且均沿竖直方向运动.爆炸时间极短...