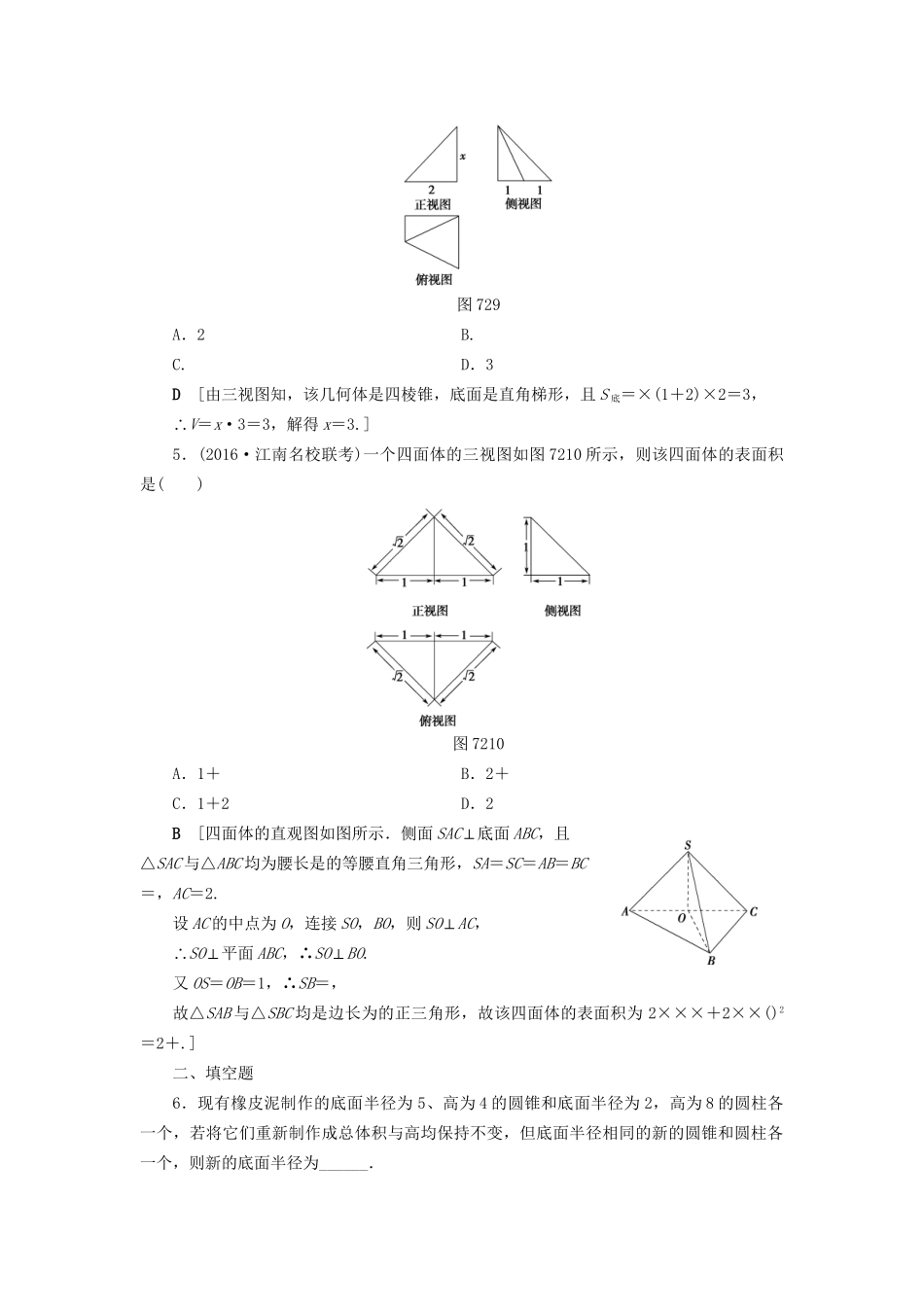
课时分层训练(三十九)空间几何体的表面积与体积A组基础达标(建议用时:30分钟)一、选择题1.已知等腰直角三角形的直角边的长为2,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为()A.B.C.2πD.4πB[依题意知,该几何体是以为底面半径,为高的两个同底圆锥组成的组合体,则其体积V=π()2×2=π.]2.已知底面边长为1,侧棱长为的正四棱柱的各顶点均在同一个球面上,则该球的体积为()【导学号:31222246】A.B.4πC.2πD.D[依题意可知正四棱柱体对角线的长度等于球的直径,可设球半径为R,则2R==2,解得R=1,所以V=R3=.]3.(2016·山东高考)一个由半球和四棱锥组成的几何体,其三视图如图728所示,则该几何体的体积为()图728A.+πB.+πC.+πD.1+πC[由三视图知,该四棱锥是底面边长为1,高为1的正四棱锥,结合三视图可得半球半径为,从而该几何体的体积为×12×1+×π×3=+π.故选C.]4.某几何体的三视图如图729所示,且该几何体的体积是3,则正视图中的x的值是()【导学号:31222247】图729A.2B.C.D.3D[由三视图知,该几何体是四棱锥,底面是直角梯形,且S底=×(1+2)×2=3,∴V=x·3=3,解得x=3.]5.(2016·江南名校联考)一个四面体的三视图如图7210所示,则该四面体的表面积是()图7210A.1+B.2+C.1+2D.2B[四面体的直观图如图所示.侧面SAC⊥底面ABC,且△SAC与△ABC均为腰长是的等腰直角三角形,SA=SC=AB=BC=,AC=2.设AC的中点为O,连接SO,BO,则SO⊥AC,∴SO⊥平面ABC,∴SO⊥BO.又OS=OB=1,∴SB=,故△SAB与△SBC均是边长为的正三角形,故该四面体的表面积为2×××+2××()2=2+.]二、填空题6.现有橡皮泥制作的底面半径为5、高为4的圆锥和底面半径为2,高为8的圆柱各一个,若将它们重新制作成总体积与高均保持不变,但底面半径相同的新的圆锥和圆柱各一个,则新的底面半径为______.【导学号:31222248】[设新的底面半径为r,由题意得×π×52×4+π×22×8=×π×r2×4+π×r2×8,∴r2=7,∴r=.]7.一个六棱锥的体积为2,其底面是边长为2的正六边形,侧棱长都相等,则该六棱锥的侧面积为________.12[设正六棱锥的高为h,棱锥的斜高为h′.由题意,得×6××2××h=2,∴h=1,∴斜高h′==2,∴S侧=6××2×2=12.]8.某几何体的三视图如图7211所示,则该几何体的体积为________.图7211π[由三视图可知,该几何体是一个圆柱和半个圆锥组合而成的几何体,其体积为π×12×2+×π×12×1=π.]三、解答题9.如图7212,在三棱锥DABC中,已知BC⊥AD,BC=2,AD=6,AB+BD=AC+CD=10,求三棱锥DABC的体积的最大值.图7212[解]由题意知,线段AB+BD与线段AC+CD的长度是定值, 棱AD与棱BC相互垂直,设d为AD到BC的距离,4分则VDABC=AD·BC×d××=2d,当d最大时,VDABC体积最大.8分 AB+BD=AC+CD=10,∴当AB=BD=AC=CD=5时,d有最大值=.此时V=2.12分10.四面体ABCD及其三视图如图7213所示,平行于棱AD,BC的平面分别交四面体的棱AB,BD,DC,CA于点E,F,G,H.图7213(1)求四面体ABCD的体积;(2)证明:四边形EFGH是矩形.[解](1)由该四面体的三视图可知,BD⊥DC,BD⊥AD,AD⊥DC,BD=DC=2,AD=1,∴AD⊥平面BDC,3分∴四面体ABCD的体积V=××2×2×1=.5分(2)证明: BC∥平面EFGH,平面EFGH∩平面BDC=FG,平面EFGH∩平面ABC=EH,8分∴BC∥FG,BC∥EH,∴FG∥EH.同理EF∥AD,HG∥AD,∴EF∥HG,∴四边形EFGH是平行四边形.又 AD⊥平面BDC,∴AD⊥BC,∴EF⊥FG.∴四边形EFGH是矩形.12分B组能力提升(建议用时:15分钟)1.(2015·全国卷Ⅰ)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图7214所示.若该几何体的表面积为16+20π,则r=()图7214A.1B.2C.4D.8B[如图,该几何体是一个半球与一个半圆柱的组合体,球的半径为r,圆柱的底面半径为r,高为2r,则表面积S=×4πr2+πr2+4r2+πr·2r=(5π+4)r2.又S=16+20π,∴(5π+4)r2=16+20π,∴r2=4,r=2,故选B.]2.三棱锥PABC中,D,E分别为PB,PC的中点,记三棱锥...