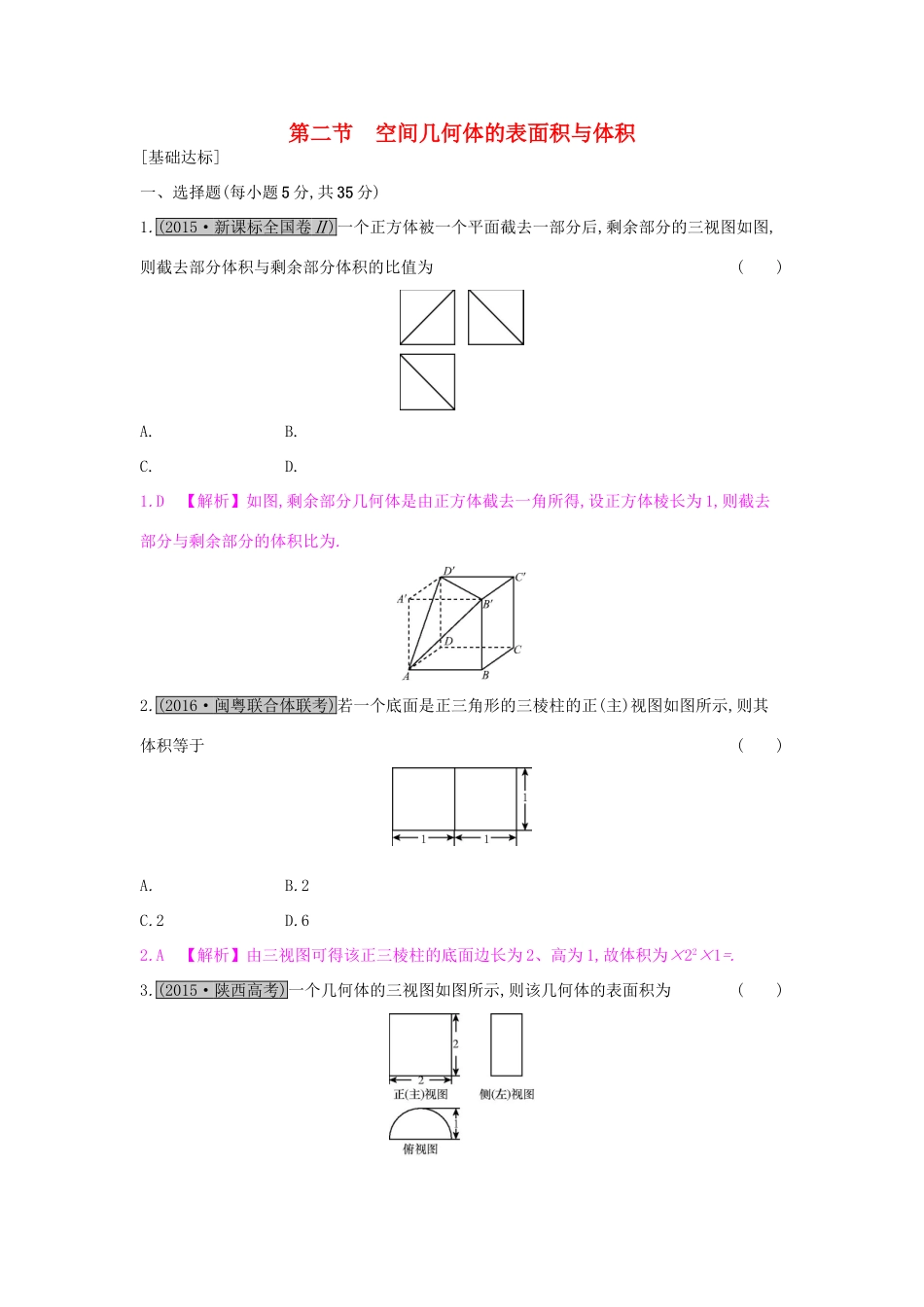
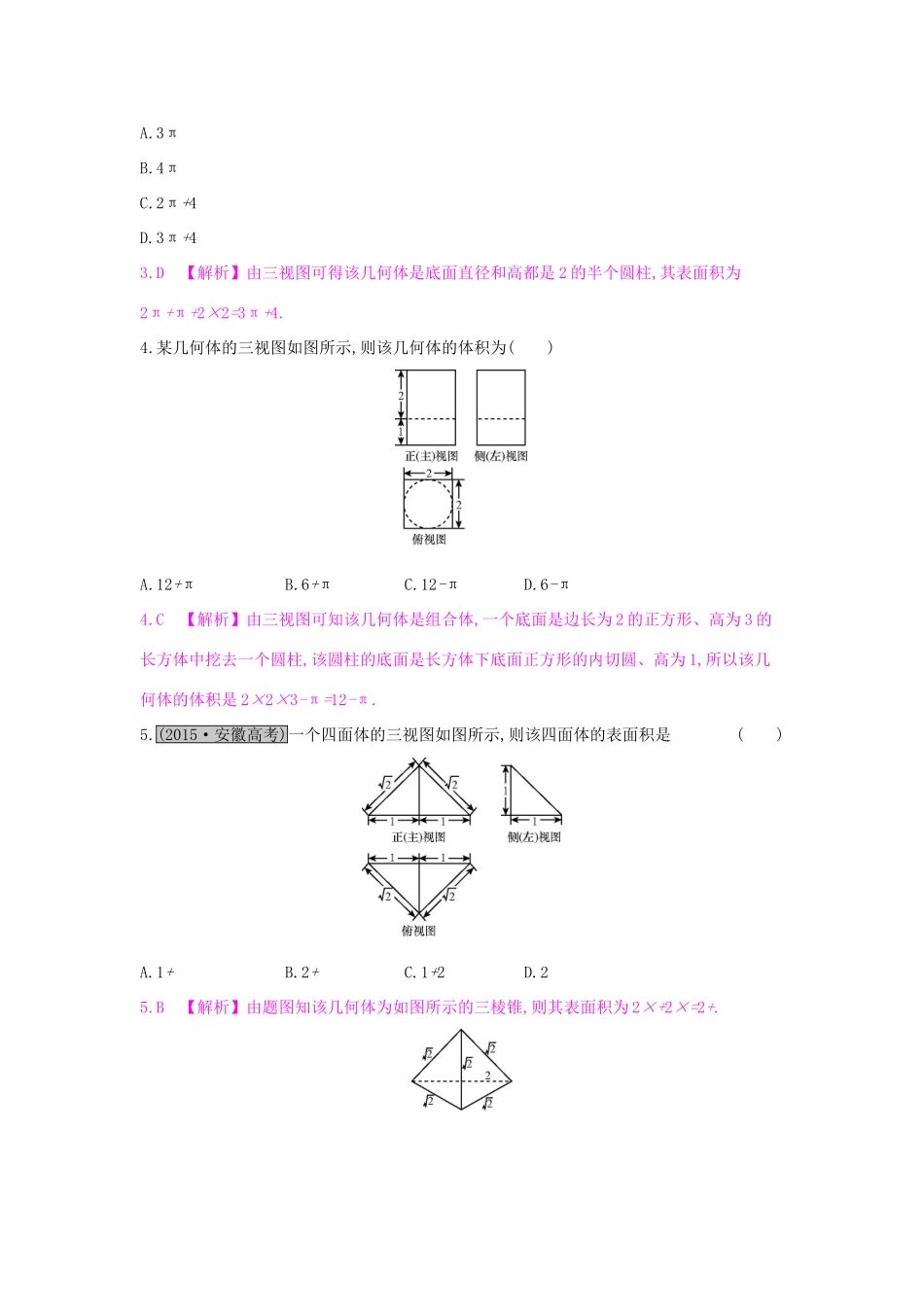
第二节空间几何体的表面积与体积[基础达标]一、选择题(每小题5分,共35分)1.(2015·新课标全国卷Ⅱ)一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为()A.B.C.D.1.D【解析】如图,剩余部分几何体是由正方体截去一角所得,设正方体棱长为1,则截去部分与剩余部分的体积比为.2.(2016·闽粤联合体联考)若一个底面是正三角形的三棱柱的正(主)视图如图所示,则其体积等于()A.B.2C.2D.62.A【解析】由三视图可得该正三棱柱的底面边长为2、高为1,故体积为×22×1=.3.(2015·陕西高考)一个几何体的三视图如图所示,则该几何体的表面积为()A.3πB.4πC.2π+4D.3π+43.D【解析】由三视图可得该几何体是底面直径和高都是2的半个圆柱,其表面积为2π+π+2×2=3π+4.4.某几何体的三视图如图所示,则该几何体的体积为()A.12+πB.6+πC.12-πD.6-π4.C【解析】由三视图可知该几何体是组合体,一个底面是边长为2的正方形、高为3的长方体中挖去一个圆柱,该圆柱的底面是长方体下底面正方形的内切圆、高为1,所以该几何体的体积是2×2×3-π=12-π.5.(2015·安徽高考)一个四面体的三视图如图所示,则该四面体的表面积是()A.1+B.2+C.1+2D.25.B【解析】由题图知该几何体为如图所示的三棱锥,则其表面积为2×+2×=2+.6.(2016·广东实验中学模拟)已知某棱锥的三视图如图所示,俯视图为正方形,根据图中所给的数据,那么该棱锥外接球的体积是()A.πB.πC.πD.π6.C【解析】由三视图可得该几何体是四棱锥,底面是边长为的正方形,一条长度为2的侧棱垂直于底面,其外接球的球心在长度为2的侧棱的中点,所以外接球的半径R=,则该球的体积为πR3=π.7.(2015·银川质检)一个四棱锥的三视图如图所示,那么这个四棱锥的表面积是()A.B.C.D.7.A【解析】由三视图可得该四棱锥的底面是上底、下底和高分别为1,2和1的直角梯形,底面积为,有一条长度为2的侧棱垂直于底面,四个侧面都是直角三角形,面积分别为1,2,,所以该四棱锥的表面积为+1+2+.二、填空题(每小题5分,共10分)8.(2015·河西五市联考)正四棱锥P-ABCD的五个顶点在同一球面上,若正四棱锥的底面边长是4,侧棱长为2,则此球的表面积.8.36π【解析】设该正四棱锥外接球的半径为R,底面中心为O,则正四棱锥的高PO=4,OA=2,则(2)2+(4-R)2=R2,解得R=3,故此球的表面积为4πR2=36π.9.(2015·天津高考)一个几何体的三视图如图所示(单位:m),则该几何体的体积为m3.9.π【解析】由三视图知该几何体由三部分组成,两边是底面半径为r=1,高为1的圆锥,中间部分是底面半径为r=1,高为2的圆柱,则其体积为V=×πr2×1×2+πr2×2=π.[高考冲关]1.(5分)(2015·银川二中二模)已知三棱锥的三视图如图所示,其正(主)视图是直角边长为2的等腰直角三角形,侧(左)视图也为直角三角形,俯视图是边长为2的等边三角形,则它的外接球表面积为()A.48πB.πC.16πD.6π1.B【解析】由三视图可得该三棱锥的底面是边长为2的正三角形,有一条长度为2的侧棱垂直于底面,底面正三角形的中心为O,OP垂直于底面,且OP=1(点P为其外接球的球心),则该球的半径R=,所以它的外接球表面积为4πR2=4π×.2.(5分)某几何体的三视图如图所示,则该几何体的体积是()A.πB.πC.πD.π2.C【解析】由三视图可得该几何体是组合体,上方是底面圆半径为1、高为的半个圆锥,下方是底面圆半径为1、高为2的圆柱,且圆柱的上底面与圆锥的底面重合,所以该几何体的体积是π×+2π=π.3.(5分)(2015·湖南高考)某工件的三视图如图所示,现将该工件通过切削,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为材料利用率=()A.B.C.D.3.A【解析】由三视图知,原工件为圆锥,要使长方体新工件的体积最大,则长方体底面为正方形,过长方体的顶点作轴截面如图,则AB为底面正方形的对角线,设长方体底面边长为a,高为h,则0
0.当a>时,S'<0,故函数S=a2h=-a3+2a2在内是增函数,在内是减函数,故当a=时,S取最大值,为-+2,圆锥的体积为×π×12×2=,故原工件的材料利用率为.4.(5分)已知三棱锥S-ABC的所有顶点都在球O的球面上,SA⊥平面ABC,...