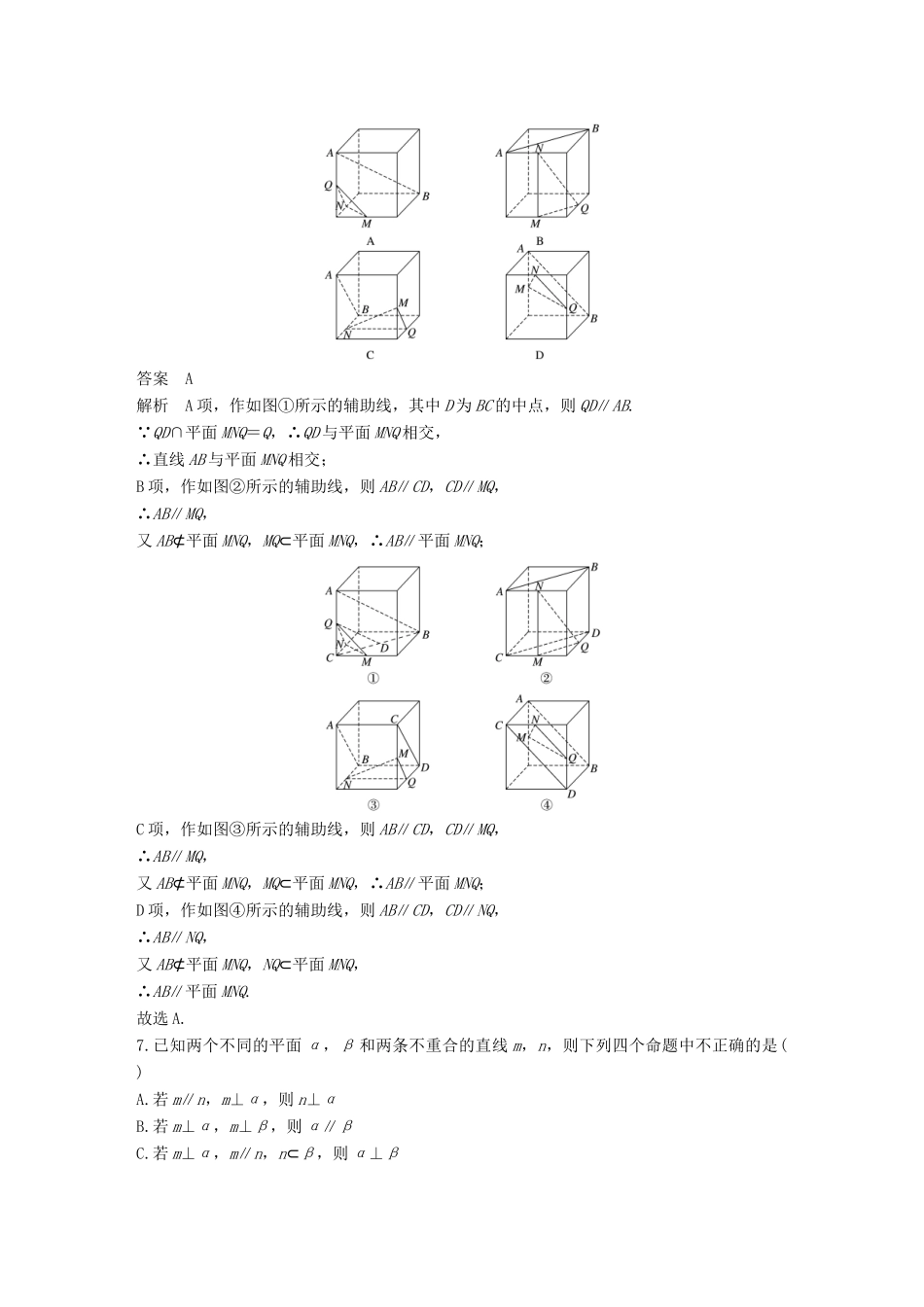
第14练空间线面关系的判断[明考情]空间线面关系的判断是高考的必考内容,主要以选择题形式出现,属于基础题.[知考向]1.空间线面位置关系的判断.2.空间中的平行、垂直关系.考点一空间线面位置关系的判断方法技巧(1)判定两直线异面的方法:①反证法;②利用结论:过平面外一点和平面内一点的直线和平面内不过该点的直线是异面直线.(2)模型法判断线面关系:借助空间几何模型,如长方体、四面体等观察线面关系,再结合定理进行判断.1.若直线l1和l2是异面直线,l1在平面α内,l2在平面β内,l是平面α与平面β的交线,则下列命题中正确的是()A.l与l1,l2都不相交B.l与l1,l2都相交C.l至多与l1,l2中的一条相交D.l至少与l1,l2中的一条相交答案D解析若l与l1,l2都不相交,则l∥l1,l∥l2,∴l1∥l2,这与l1和l2异面矛盾,∴l至少与l1,l2中的一条相交.2.(2017·常德一中模拟)已知α,β是两个不同的平面,l,m是两条不同的直线,且l⊂α,m⊂β,则()A.若α∥β,则l∥mB.若l∥m,则α∥βC.若α⊥β,则l⊥mD.若l⊥β,则α⊥β答案D解析选项A,若α∥β,则直线l,m平行或异面,错误;选项B,若l∥m,则平面α,β平行或相交,错误;选项C,若α⊥β,则直线l,m平行、相交或异面,错误;选项D,若l⊥β,则由面面垂直的判定定理可得α⊥β,正确,故选D.3.已知直线a与平面α,β,α∥β,a⊂α,点B∈β,则在β内过点B的所有直线中()A.不一定存在与a平行的直线B.只有两条a平行的直线C.存在无数条与a平行的直线D.存在唯一一条与a平行的直线答案D解析在平面内过一点,只能作一条直线与已知直线平行.4.将正方体的纸盒展开如图,直线AB,CD在原正方体的位置关系是()A.平行B.垂直C.相交成60°角D.异面且成60°角答案D解析如图,直线AB,CD异面.因为CE∥AB,所以∠ECD即为直线AB,CD所成的角,因为△CDE为等边三角形,故∠ECD=60°.5.已知α,β表示平面,m,n表示直线,m⊥β,α⊥β,给出下列四个结论:①∀n⊂α,n⊥β;②∀n⊂β,m⊥n;③∀n⊂α,m∥n;④∃n⊂α,m⊥n.则上述结论中正确的个数为()A.1B.2C.3D.4答案B解析由于m⊥β,α⊥β,所以m⊂α或m∥α.∀n⊂α,n⊥β或n与β斜交或n∥β,所以①不正确;∀n⊂β,m⊥n,所以②正确;∀n⊂α,m与n可能平行、相交或异面,所以③不正确;当m⊂α或m∥α时,∃n⊂α,m⊥n,所以④正确.考点二空间中的平行、垂直关系方法技巧(1)利用平面图形中的线的平行判断平行关系:①比例线求证平行,特别是三角形中位线定理;②平行四边形的对边互相平行;③同一平面内垂直于同一直线的两直线互相平行.(2)熟练把握平面图形中的垂直关系①等腰三角形的底边上的中线和高重合;②菱形的对角线互相垂直;③圆的直径所对的圆周角为直角;④勾股定理得垂直.(3)空间中平行与垂直的实质是转化与化归思想在空间中的体现.6.(2017·全国Ⅰ)如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是()答案A解析A项,作如图①所示的辅助线,其中D为BC的中点,则QD∥AB. QD∩平面MNQ=Q,∴QD与平面MNQ相交,∴直线AB与平面MNQ相交;B项,作如图②所示的辅助线,则AB∥CD,CD∥MQ,∴AB∥MQ,又AB⊄平面MNQ,MQ⊂平面MNQ,∴AB∥平面MNQ;C项,作如图③所示的辅助线,则AB∥CD,CD∥MQ,∴AB∥MQ,又AB⊄平面MNQ,MQ⊂平面MNQ,∴AB∥平面MNQ;D项,作如图④所示的辅助线,则AB∥CD,CD∥NQ,∴AB∥NQ,又AB⊄平面MNQ,NQ⊂平面MNQ,∴AB∥平面MNQ.故选A.7.已知两个不同的平面α,β和两条不重合的直线m,n,则下列四个命题中不正确的是()A.若m∥n,m⊥α,则n⊥αB.若m⊥α,m⊥β,则α∥βC.若m⊥α,m∥n,n⊂β,则α⊥βD.若m∥α,α∩β=n,则m∥n答案D解析易知A,B正确;对于C,因为m⊥α,m∥n,所以n⊥α.又n⊂β,所以β⊥α,即C正确;对于D,因为m∥α,α∩β=n,所以m∥n或m与n是异面直线,故D不正确.8.(2017·全国Ⅲ)在正方体ABCD-A1B1C1D1中,E为棱CD的中点,则()A.A1E⊥DC1B.A1E⊥BDC.A1E⊥BC1D.A1E⊥AC答案C解析方法一如图, A1E在平面ABCD上的射影为AE,...