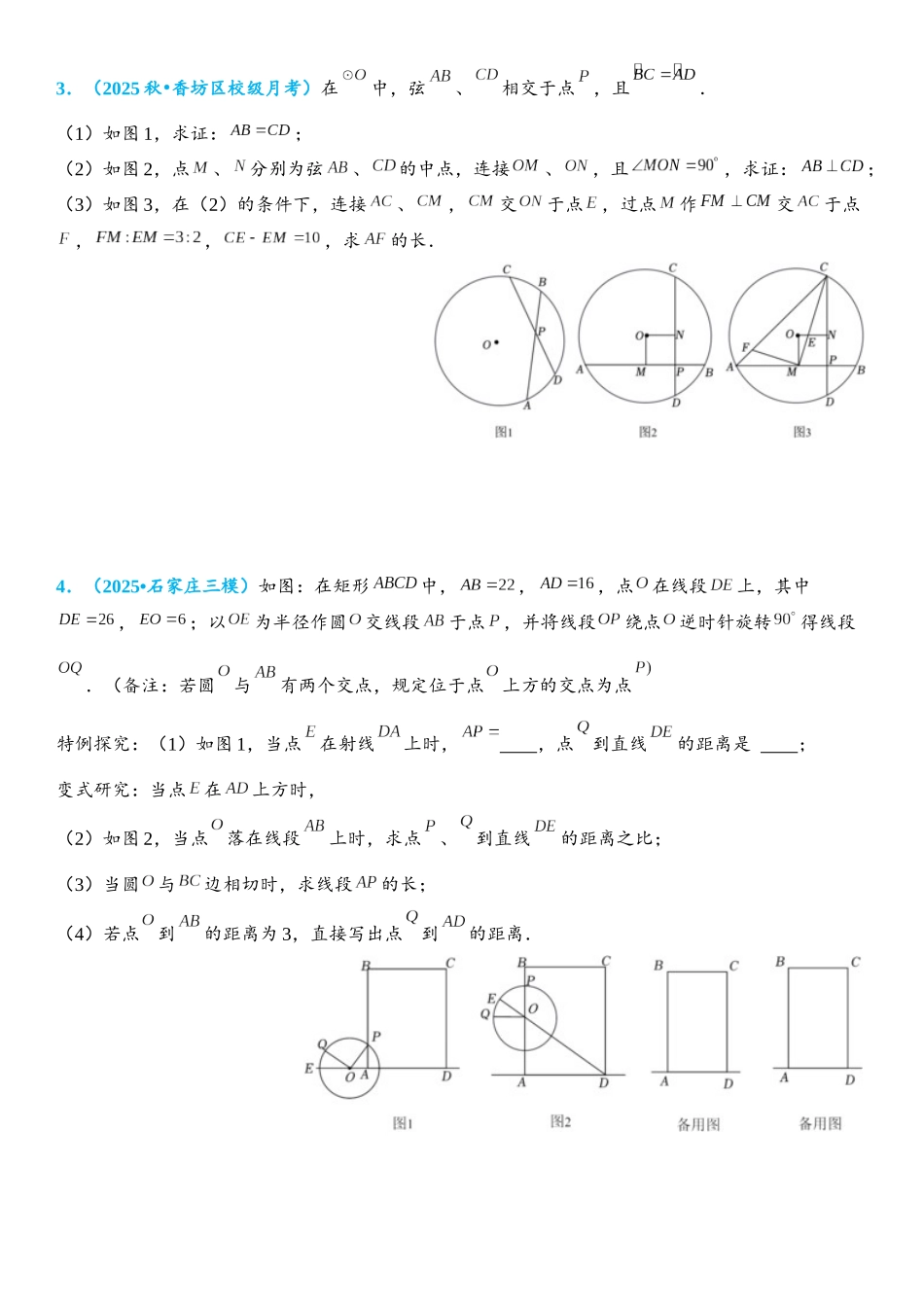
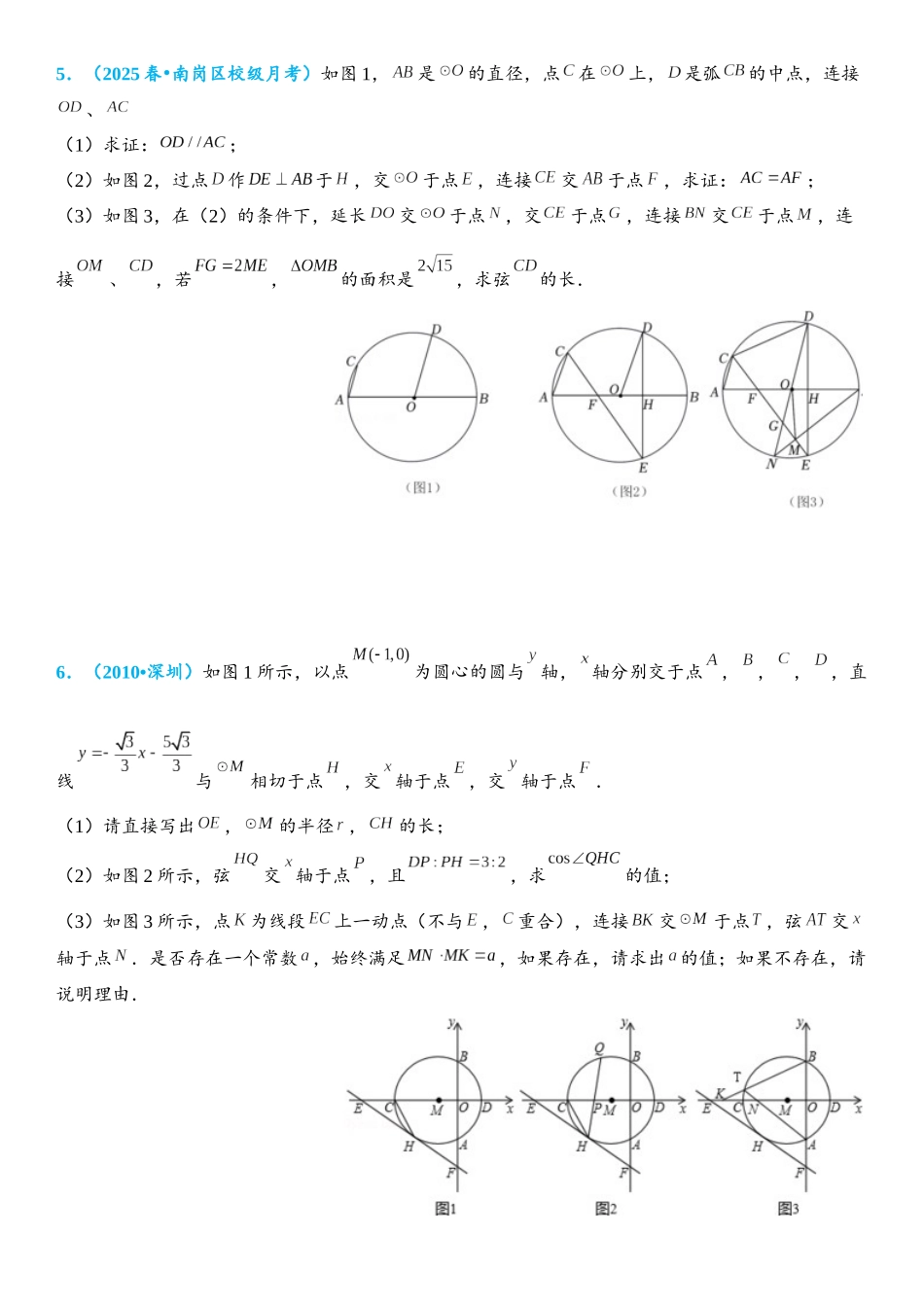
垂径定理1.(2025•南岗区二模)圆内接,是圆的切线,点为切点,.(1)如图 1,连接,求证:;(2)如图 2,当为直径,点在弧上,连接、、时;求证:.(3)如图 3,在(2)的条件下,连接与交于点,连延长与交于点,,,求的长.2.(2025•镇海区校级二模)如图,为等腰三角形的外接圆,,延长交于点,过点作垂直交于点,交于点,交于点,连结,若.(1)求证:.(2)如图 1,若,求的面积.(3)如图 2,若,求的长.3.(2025 秋 香坊区校级月考)•在中,弦、相交于点,且.(1)如图 1,求证:;(2)如图 2,点、分别为弦、的中点,连接、,且,求证:;(3)如图 3,在(2)的条件下,连接、,交于点,过点作交于点,,,求的长.4.(2025•石家庄三模)如图:在矩形中,,,点在线段上,其中,;以为半径作圆交线段于点,并将线段绕点逆时针旋转得线段.(备注:若圆与有两个交点,规定位于点上方的交点为点特例探究:(1)如图 1,当点在射线上时, ,点到直线的距离是 ;变式研究:当点在上方时,(2)如图 2,当点落在线段上时,求点、到直线的距离之比;(3)当圆与边相切时,求线段的长;(4)若点到的距离为 3,直接写出点到的距离.5.(2025 春 南岗区校级月考)•如图 1,是的直径,点在上,是弧的中点,连接、(1)求证:;(2)如图 2,过点作于,交于点,连接交于点,求证:;(3)如图 3,在(2)的条件下,延长交于点,交于点,连接交于点,连接、,若,的面积是,求弦的长.6.(2010•深圳)如图 1 所示,以点为圆心的圆与轴, 轴分别交于点,,,,直线与相切于点,交 轴于点,交轴于点.(1)请直接写出,的半径 ,的长;(2)如图 2 所示,弦交 轴于点,且,求的值;(3)如图 3 所示,点为线段上一动点(不与,重合),连接交于点,弦交轴于点.是否存在一个常数 ,始终满足,如果存在,请求出 的值;如果不存在,请说明理由.7.内接于,点在上,连接,交边于点,且.(1)如图 1,求证:;(2)如图 2,点在上,连接,交弦于点,交边于点,连接,交边于点,若,求证:;(3)如图 3,在(2)的条件下,当点在边上时,连接,交边于点,点在线段上,连接并延长,交于点,连接、,若,,,求弦的长.8.(2025•南岗区一模)已知内接于,是直径,过点作的切线.(1)如图 1,求证:;(2)如图 2,当是弧的中点时,过点作于.求证:;(3)如图 3,在(2)的条件下,与相交...