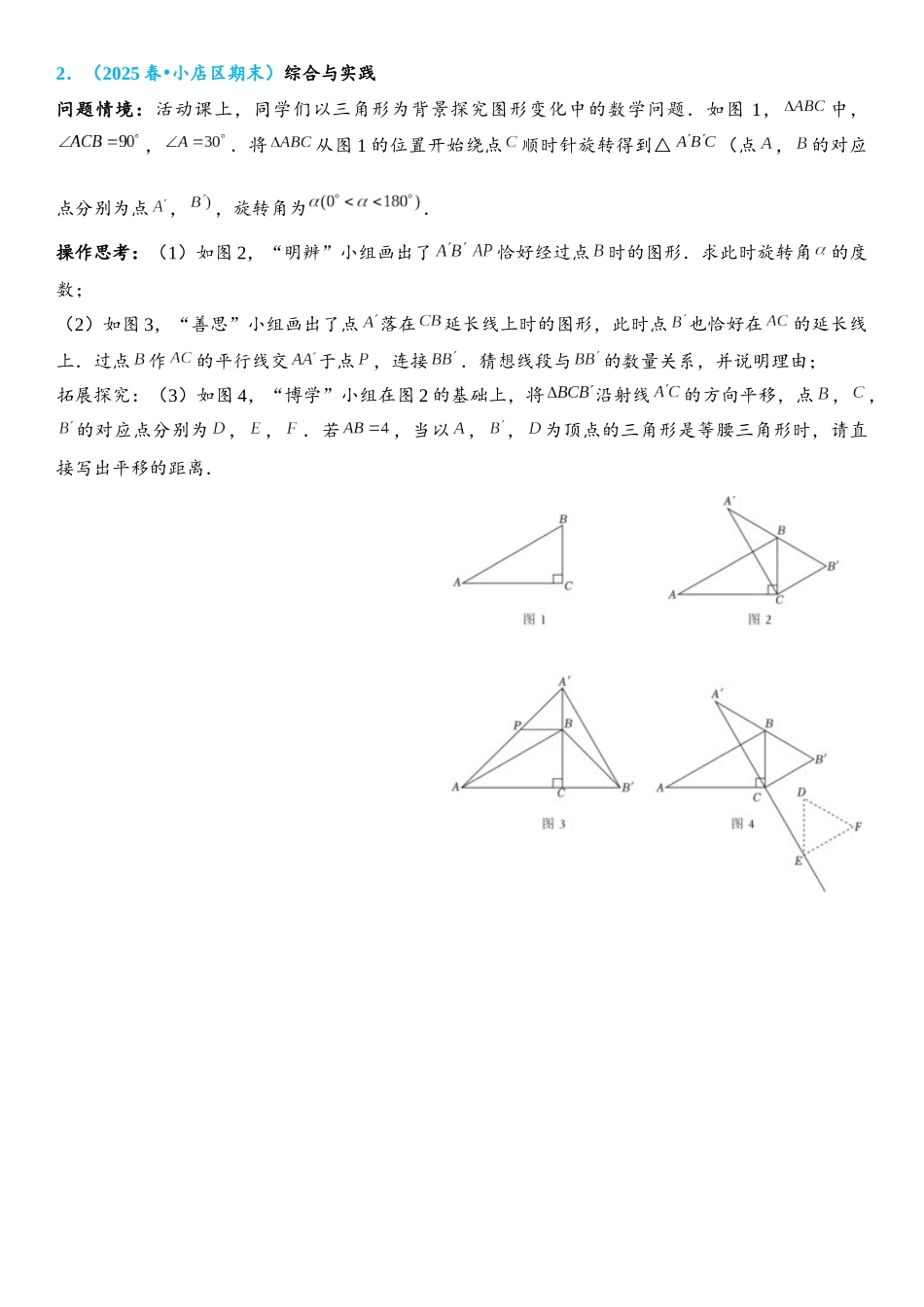
分类讨论思想1.(2025 秋 丰都县期末)•如图 1,在平面直角坐标系中,抛物线经过,与轴交于点,经过点的直线与抛物线交于另一点,点为抛物线的顶点,抛物线的对称轴与 轴交于点.(1)求直线的解析式;(2)如图 2,点为直线上方抛物线上一动点,连接,.当的面积最大时,求点的坐标以及面积的最大值.(3)如图 3,将点右移一个单位到点,连接,将(1)中抛物线沿射线平移得到新抛物线,经过点,的顶点为点,在新抛物线的对称轴上是否存在点,使得是等腰三角形?若存在,请直接写出点的坐标;若不存在,请说明理由.2.(2025 春 小店区期末)•综合与实践问题情境:活动课上,同学们以三角形为背景探究图形变化中的数学问题.如图 1,中,,.将从图 1 的位置开始绕点顺时针旋转得到△(点,的对应点分别为点,,旋转角为.操作思考:(1)如图 2,“明辨”小组画出了恰好经过点时的图形.求此时旋转角的度数;(2)如图 3,“善思”小组画出了点落在延长线上时的图形,此时点也恰好在的延长线上.过点作的平行线交于点,连接.猜想线段与的数量关系,并说明理由;拓展探究:(3)如图 4,“博学”小组在图 2 的基础上,将沿射线的方向平移,点,,的对应点分别为,,.若,当以,,为顶点的三角形是等腰三角形时,请直接写出平移的距离.3.(2025•济南模拟)如图,抛物线与 轴交于点,点,点是抛物线的顶点,过点作 轴的垂线,垂足为点.(1)求抛物线所对应的函数解析式;(2)如图 1,点是抛物线上一点,且位于 轴上方,横坐标为,连接,若,求的值;(3)如图 2,将抛物线平移后得到顶点为的抛物线.点为抛物线上的一个动点,过点作轴的平行线,交抛物线于点,过点作 轴的平行线,交抛物线于点.当以点,,为顶点的三角形与全等时,请直接写出点的坐标.4.(2025 秋 宁海县校级期中)•如图,在中,,,,若动点从点开始,按的路径运动,且速度为每秒,设出发的时间为 秒.(1)出发 2 秒后,求的周长.(2)问 为何值时,为等腰三角形?(3)另有一点,从点开始,按的路径运动,且速度为每秒,若、两点同时出发,当、中有一点到达终点时,另一点也停止运动.当 为何值时,直线把的周长分成相等的两部分?5.(2025 秋 锦江区校级月考)•如图 1,在中,,,为的中点,连结.过点作射线,为射线上一动点.(1)求的长和的面积;(2)如图 2,连结交于点,连结,作点关于的对称点,当点恰好落在的边上...