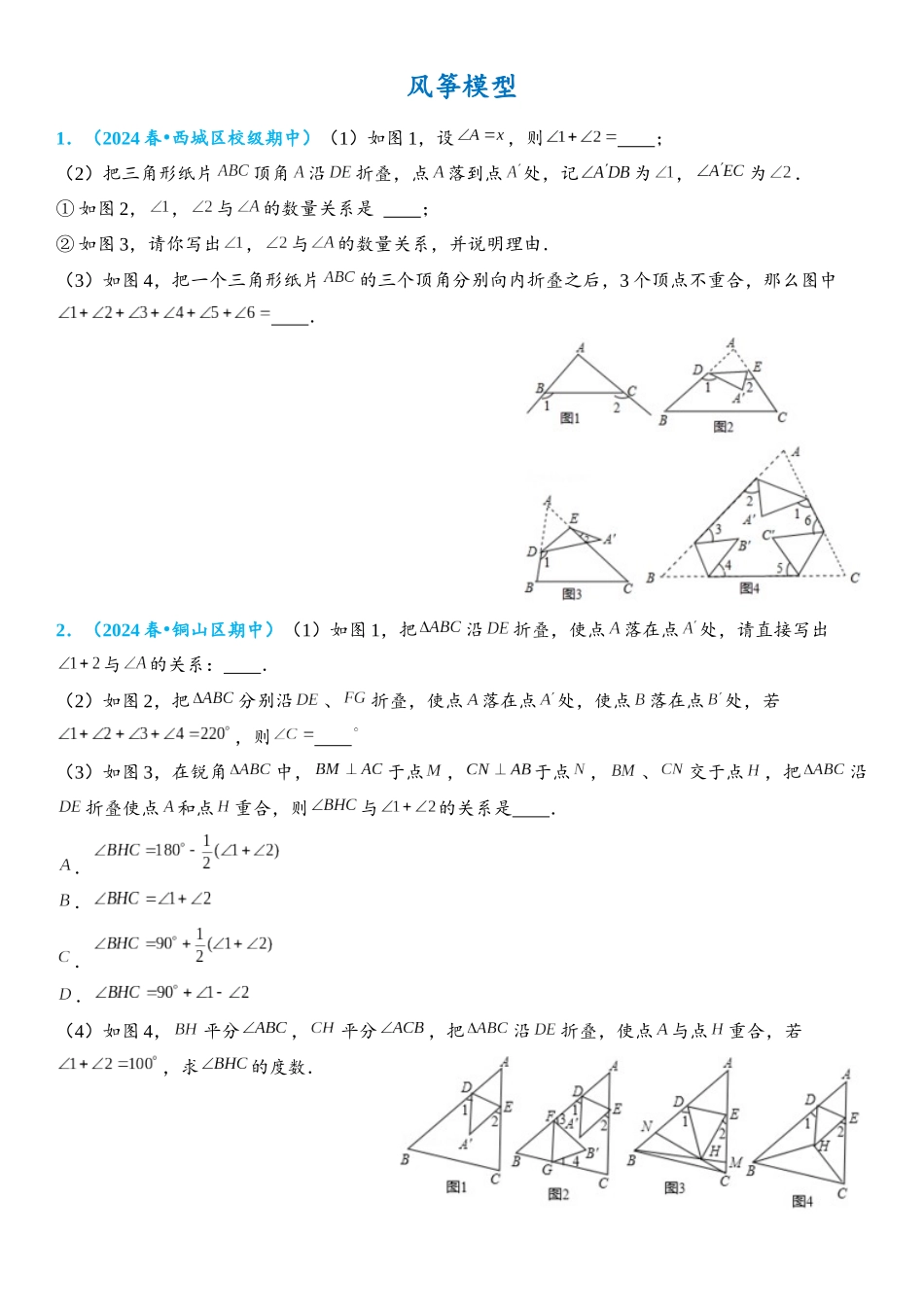
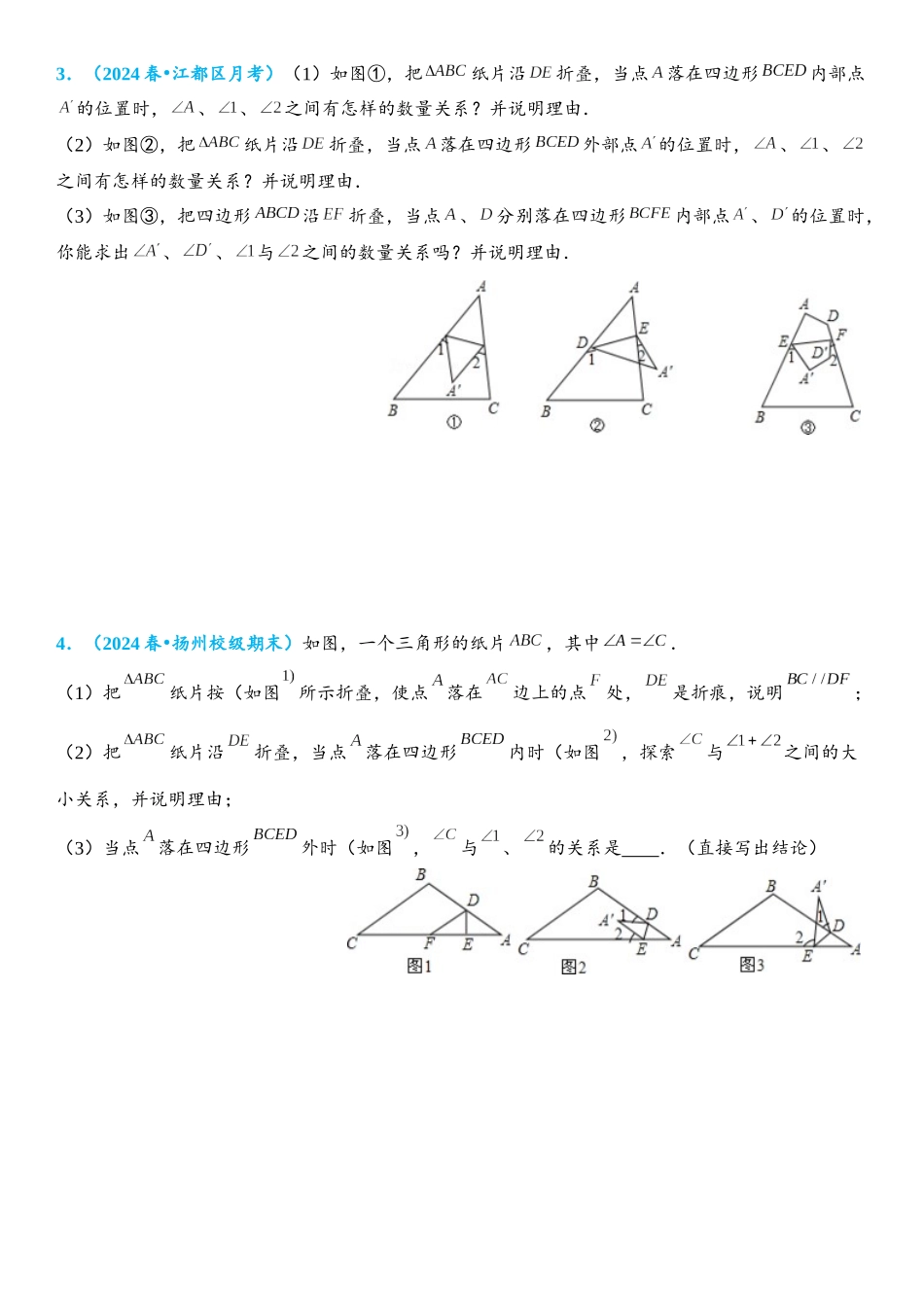
风筝模型1.(2024 春 西城区校级期中)•(1)如图 1,设,则 ;(2)把三角形纸片顶角沿折叠,点落到点处,记为,为.① 如图 2,,与的数量关系是 ;② 如图 3,请你写出,与的数量关系,并说明理由.(3)如图 4,把一个三角形纸片的三个顶角分别向内折叠之后,3 个顶点不重合,那么图中 .2.(2024 春 铜山区期中)•(1)如图 1,把沿折叠,使点落在点处,请直接写出与的关系: .(2)如图 2,把分别沿、折叠,使点落在点处,使点落在点处,若,则 (3)如图 3,在锐角中,于点,于点,、交于点,把沿折叠使点和点重合,则与的关系是 .....(4)如图 4,平分,平分,把沿折叠,使点与点重合,若,求的度数.3.(2024 春 江都区月考)•(1)如图①,把纸片沿折叠,当点落在四边形内部点的位置时,、、之间有怎样的数量关系?并说明理由.(2)如图②,把纸片沿折叠,当点落在四边形外部点的位置时,、、之间有怎样的数量关系?并说明理由.(3)如图③,把四边形沿折叠,当点、分别落在四边形内部点、的位置时,你能求出、、与之间的数量关系吗?并说明理由.4.(2024 春 扬州校级期末)•如图,一个三角形的纸片,其中.(1)把纸片按(如图所示折叠,使点落在边上的点处,是折痕,说明;(2)把纸片沿折叠,当点落在四边形内时(如图,探索与之间的大小关系,并说明理由;(3)当点落在四边形外时(如图,与、的关系是 .(直接写出结论)5.(2024 春 宜兴市校级月考)•操作:折叠纸片,并将折叠后的部分压平在纸片原来所在平面内.研究一:(1)将纸片沿直线折叠成图 1 的形状,则、与之间的数量关系为 (不需要说明理由).(2)将纸片沿直线折成图 2 的形状,则、和之间存在怎样的数量关系?请试着找出来,并说明理由.研究二:将四边形与不平行)沿直线折叠成图 3 的形状,则、与、之间的数量关系是 (请将含、的项放在等式的左边,其余各项放在等式的右边),并说明理由.6.(2024 春 姜堰市期中)•,直线交于,交于,将沿折叠,使落在同一平面上的处,的两边与、的夹角分别记为,如图①,当落在四边形内部时,探索与之间的数量关系,并说明理由.如图②,当落在下方时,请直接写出与之间的数量关系.如图③,当落在右侧时,探索与,之间的数量关系,并说明理由.7.(2025 秋 永春县期中)•如图 1,在中,,,点在线段上(不与点、点重合),以为腰作等腰直角,于点.(1)...