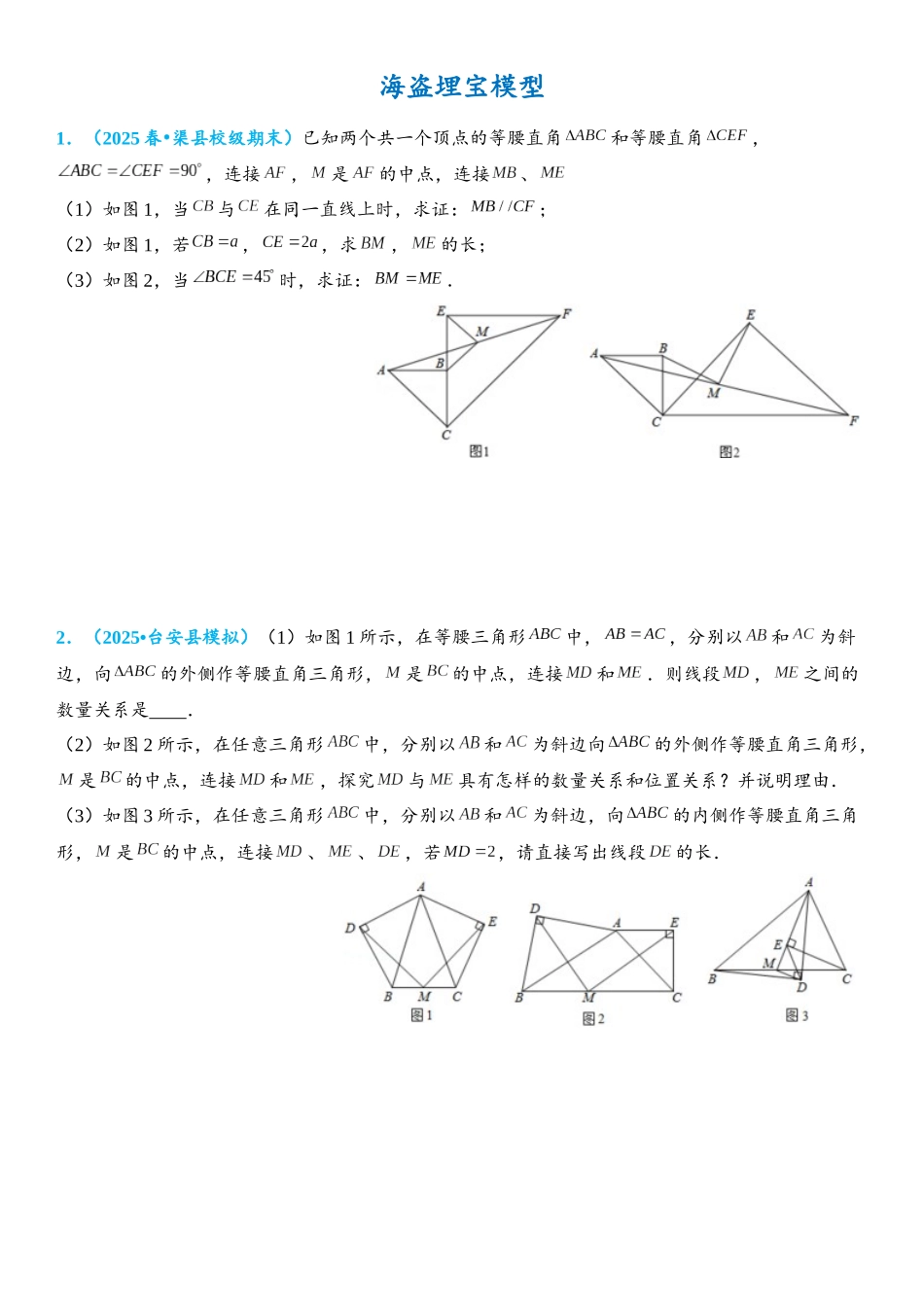
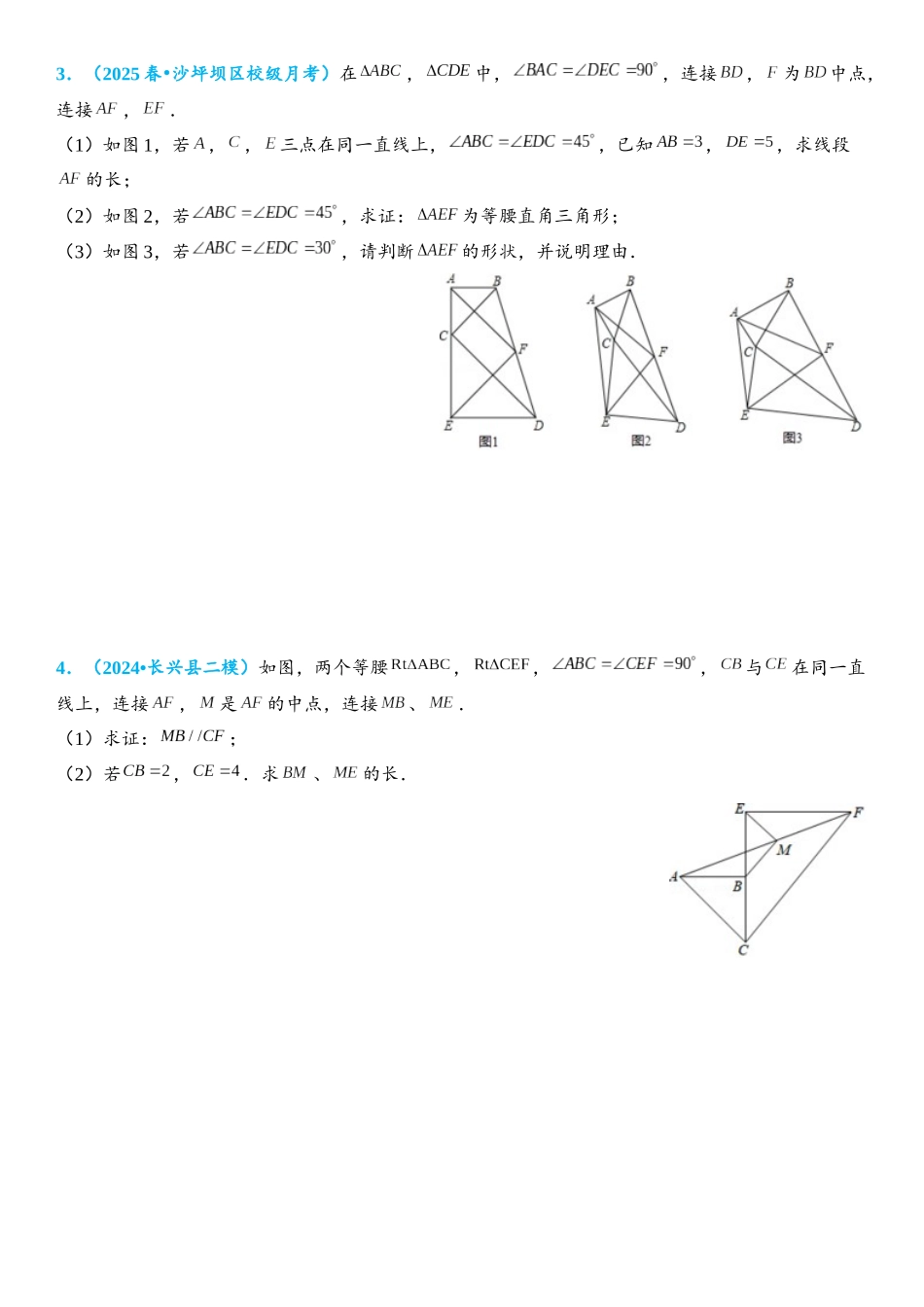
海盗埋宝模型1.(2025 春 渠县校级期末)•已知两个共一个顶点的等腰直角和等腰直角,,连接,是的中点,连接、(1)如图 1,当与在同一直线上时,求证:;(2)如图 1,若,,求,的长;(3)如图 2,当时,求证:.2.(2025•台安县模拟)(1)如图 1 所示,在等腰三角形中,,分别以和为斜边,向的外侧作等腰直角三角形,是的中点,连接和.则线段,之间的数量关系是 .(2)如图 2 所示,在任意三角形中,分别以和为斜边向的外侧作等腰直角三角形,是的中点,连接和,探究与具有怎样的数量关系和位置关系?并说明理由.(3)如图 3 所示,在任意三角形中,分别以和为斜边,向的内侧作等腰直角三角形,是的中点,连接、、,若,请直接写出线段的长.3.(2025 春 沙坪坝区校级月考)•在,中,,连接,为中点,连接,.(1)如图 1,若,,三点在同一直线上,,已知,,求线段的长;(2)如图 2,若,求证:为等腰直角三角形;(3)如图 3,若,请判断的形状,并说明理由.4.(2024•长兴县二模)如图,两个等腰,,,与在同一直线上,连接,是的中点,连接、.(1)求证:;(2)若,.求、的长.5.(2025•沂源县一模)已知如图 1,在中,,,点在上,交于,点是的中点(1)写出线段与线段的关系并证明;(2)如图 2,将绕点逆时针旋转,其它条件不变,线段与线段的关系是否变化,写出你的结论并证明;(3)将绕点逆时针旋转一周,如果,,直接写出线段的范围.6.(2025 秋 荔城区校级期末)•如图,四边形是正方形,点为对角线的中点.(1)问题解决:如图①,连接,分别取,的中点,,连接,则与的数量关系是 ,位置关系是 .(2)问题探究:如图②,将图①中的绕点按顺时针方向旋转得到△,连接,点,分别为,的中点,连接,.试判断与之间的数量关系,并证明;(3)拓展延伸:如图③,将图①中的绕点按逆时针方向旋转得到△,连接,点,分别为,的中点,连接,.若正方形的边长为 1,求线段的长7.(2025 春 沙坪坝区校级期末)•如图,已知,边的中点,(1)分别以和为腰,向的外侧作等腰三角形,其中,,且,如图 1 所示.① 若,求的度数;② 求证:;(2)分别以和为斜边,向的外侧作等腰直角三角形,其中,如图 2所示,连接和,则和具有怎样的数量和位置关系?请给出证明过程.8.(2025•越秀区校级模拟)在中,,.点在边上(不与,重合),连接,为中点.(1)若过点作于,连接、、,如图 1...