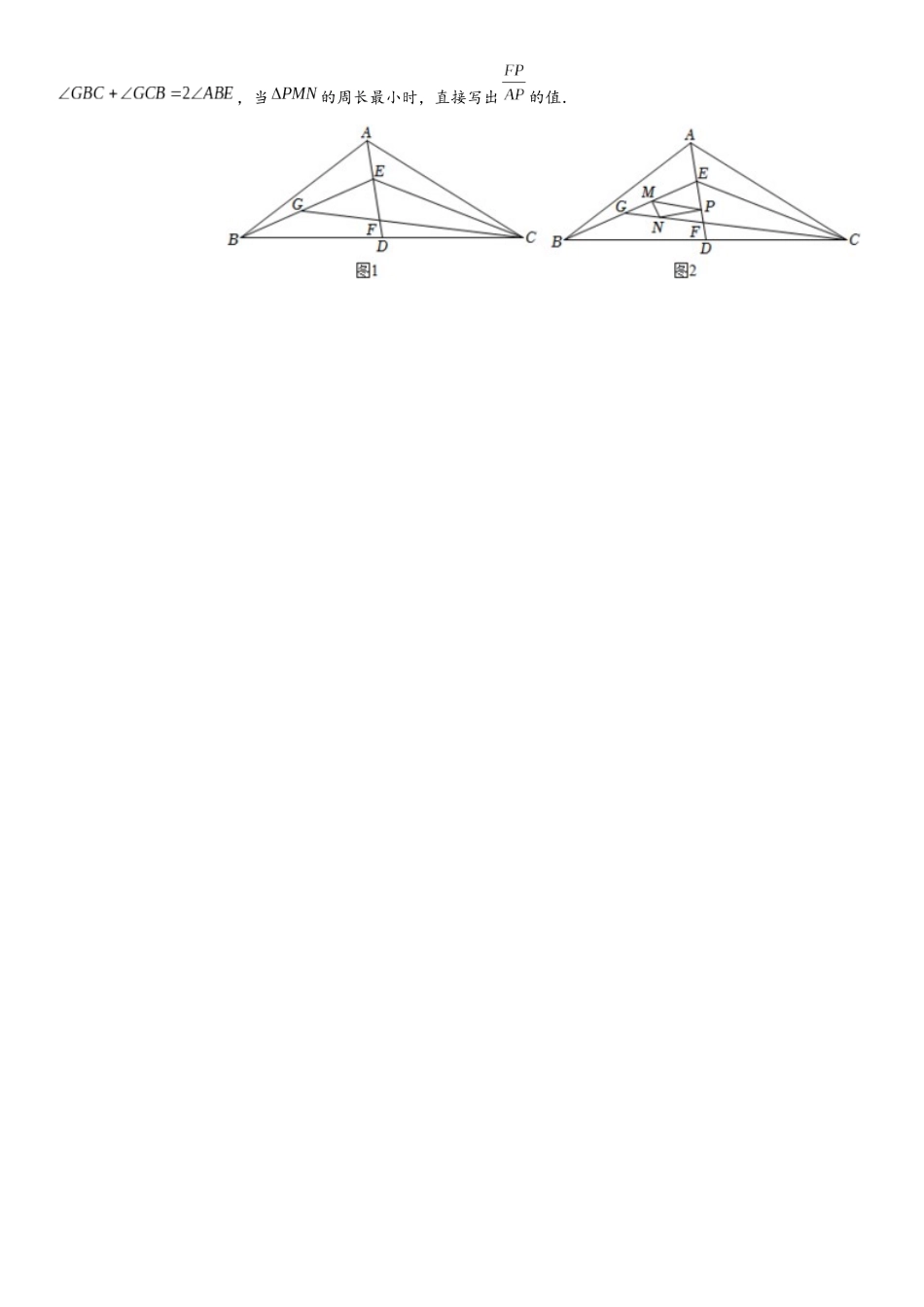
将军饮马(2)1.(2025•安国市一模) 问题提出初中数学的学习中,我们学习了“两点之间线段最短”“垂线段最短”等知识常可利用它们来解决“最值问题”.简单运用(1)如图 1,在中,,,,在上取一点,则的长的最小值是 .综合运用(2)如图 1,在中,,,,在、、上分别取点、、,使得的周长最小.画出图形确定、、的位置,并直接写出的周长的最小值.拓展延伸(3)图 2 是由线段、线段、组成的图形,其中,,,为,分别在、线段和线段.上取点、、,使得的周长最小,画出图形确定、、的位置,并直接写出的周长的最小值.2.(2025 春 泗水县期末)•将直角坐标系中一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形(也称为直线的坐标三角形).如图,一次函数的图象与、轴分别交于点、,那么为此一次函数的坐标三角形(也称为直线的坐标三角形).(1)如果点在轴上,将沿着直线翻折,使点落在点上,求直线的坐标三角形的面积;(2)如果一次函数的坐标三角形的周长是 21,求值;(3)在(1)(2)条件下,如果点的坐标是,直线上有一点,使得周长最小,求此时的面积.3.(2025 春 江岸区校级月考)•如图 1,直线与轴交于点,与轴交于点,把直线沿直线折叠,使点落在轴负半轴上的点处,折痕与轴交于点.(1)试求点、、的坐标;(2)点是直线上的一个动点,且的面积为 4,求点的坐标;(3)如图 2,点为直线上的一个动点,将线段绕点顺时针旋转后得到线段,求的最小值.4.(2025 春 沙坪坝区校级期末)•如图 1,在中,是边上的中线,点、在上,连接,,,延长交于点.(1)若,,则 ;(2)若,.求证:;( 3 ) 如 图 2 , 在 ( 2 ) 条 件 下 , 点、、分 别 是三 边 上 的 动 点 , 且,,当的周长最小时,直接写出的值.5.(2025 春 安新县期末)•李明酷爱数学,勤于思考,善于反思.在学习八年级下册数学知识之后,他发现“二次根式、勾股定理、一次函数、平行四边形”都和“将军饮马”问题有关联,并且为解决“饮马位置”“最短路径长”等问题,提供了具体的数学方法.于是他撰写了一篇数学作文.请你认真阅读思考,帮助李明完成相关问题.“将军饮马”问题的探究与拓展—八年级三班李明“白日登山望烽火,黄昏饮马傍交河”(唐 李颀《古从军行》 ,这句诗让我想到了有趣的“将军饮马”问题:将军从地出发到河边 饮马,然后再到地军营视察,怎样走路径最短?【...