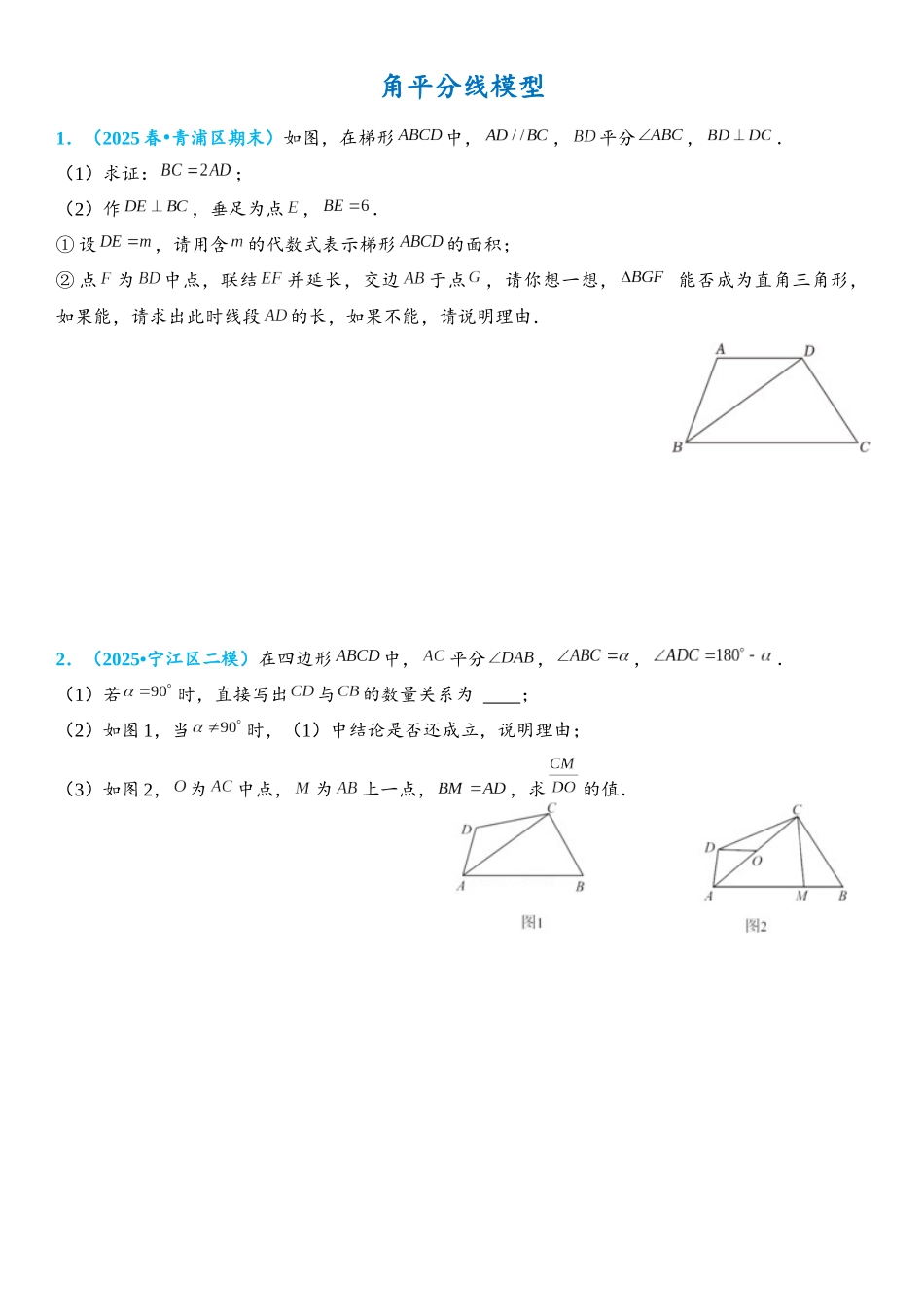
角平分线模型1.(2025 春 青浦区期末)•如图,在梯形中,,平分,.(1)求证:;(2)作,垂足为点,.① 设,请用含的代数式表示梯形的面积;② 点为中点,联结并延长,交边于点,请你想一想, 能否成为直角三角形,如果能,请求出此时线段的长,如果不能,请说明理由.2.(2025•宁江区二模)在四边形中,平分,,.(1)若时,直接写出与的数量关系为 ;(2)如图 1,当时,(1)中结论是否还成立,说明理由;(3)如图 2,为中点,为上一点,,求的值.3.(2025 春 二道区校级期中)•【问题】如图①,在中,,平分,平分.求的度数,对于上述问题,在以下解答过程的空白处填上适当的内容(理由或数学式).解:(三角形内角和. (等式性质). (已知), (等量代换).平分(已知),(角平分线的定义).同理, ; (等式性质)., (等式性质).【拓展】如图②,在中,,平分,平分.则 .【应用】如图③,在中,平分,平分,平分,平分.若,则 .4.(2025 春 渝中区校级期中)•在中,为边上一点,连接,为上一点,连接,(1)如图 1,延长交于点,若平分,平分,,,,求的周长;(2)如图 2,连接,若,,为中点,连接,请猜想线段,,之间的数量关系,并证明你的猜想;(3)如图 3,在第(2)问的条件下,当时,点是直线上一动点,连接,将沿着翻折得,连接,为的中点,连接,当点到的距离最小时,直接写出的值.5.(2025 秋 南关区校级月考)•【感知】如图①所示,在等腰中,,平分,易得(不需要证明).【探究】如图②所示,李丽同学将图①的等腰改为任意,平分,他通过观察、测量,猜想仍然成立,为了证明自己的猜想,他与同学进行交流讨论,得到了证明猜想的两种方法:方法 1:过点分别作:于点,于点,利用与的面积比证明结论.方法 2:过点作交延长线于点,利用与相似证明结论.请你参考上面的两种方法,选择其中的一种方法完成证明.【应用】如图③所示,在中,,,,平分.若点在边上,,交于点,则 .6.(2025 春 丹阳市期末)•【阅读材料】像,,,,两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式.例如,与,与,与,,等都是互为有理化因式.进行二次根式计算时,利用有理化因式,可以化去分母中的根号.【解决问题】(1)的有理化因式为 ;(2)化简:;(3)①如图 1,中,,,,点到边的距离为 ;② 如图 2,中,与的角平分...