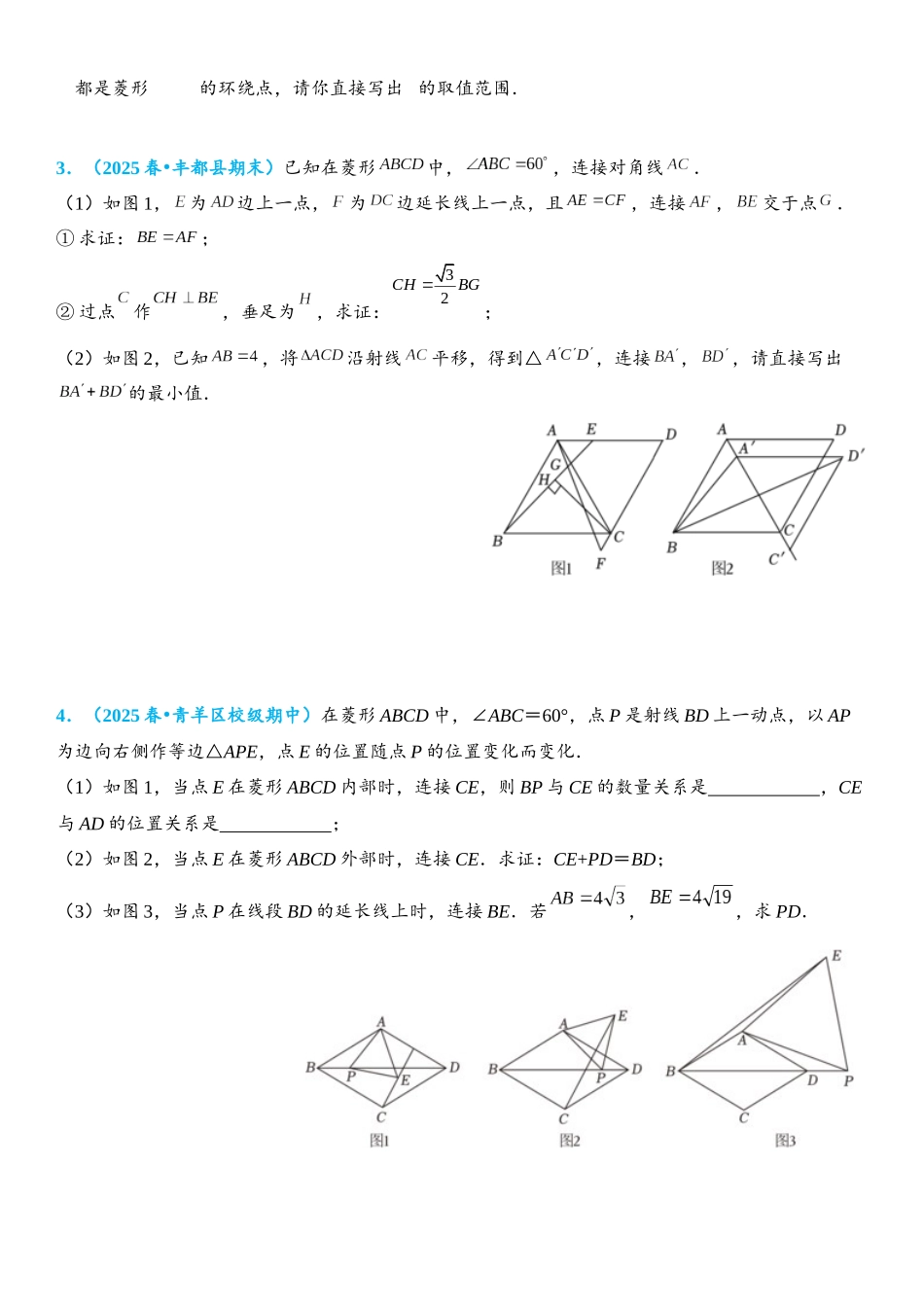
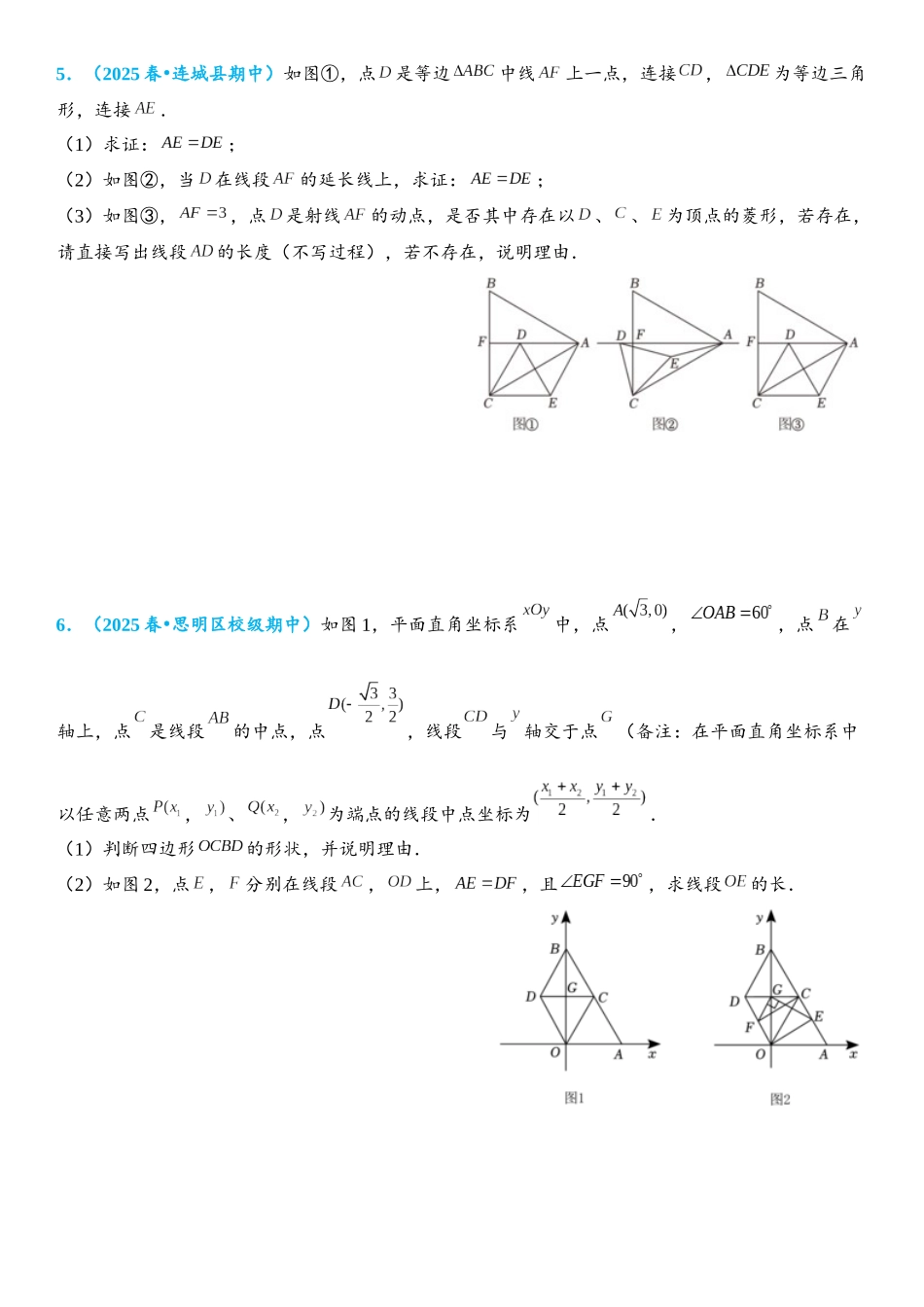
菱形综合题1.(2025•宽城区校级开学)如图,在△ABC 中,BA=BC=10,BC 边上高为 8,点 D 为边 BC 的中点,点 P 从点 B 出发,沿折线 BA﹣AC 向点 C 运动,在 BA、AC 上的速度分别为每秒 5 个单位长度和每秒个单位长度.当点 P 不与点 A 重合时,连接 PD,以 PA、PD 为邻边作▱APDE.设点 P的运动时间为 t 秒(t>0).(1)①线段 AC 的长为 ;② 用含 t 的代数式表示线段 AP 的长;(2)当点 E 在△ABC 内部时,求 t 的取值范围;(3)当▱APDE 是菱形时,求 t 的值;(4)作点 B 关于直线 PD 的对称点 B′,连接 B′D,当 B′D⊥BC 时,直接写出 t 的值.2.(2025 春 丰台区期末)•在平面直角坐标系中,对于点和菱形,给出如下定义:若菱形上存在一点,使点绕点逆时针旋转的对应点在菱形的较短的一条对角线上,则称点为菱形的环绕点.图 1 为菱形的环绕点的示意图.如图,设菱形的中心为,,点和点都在 轴上,且.(1)在点,,中,菱形的环绕点是 ;(2)若为菱形的环绕点,求 的取值范围;(3)设正方形以点为中心,各边均与坐标轴平行,边长为.若正方形上任意一点都是菱形的环绕点,请你直接写出 的取值范围.3.(2025 春 丰都县期末)•已知在菱形中,,连接对角线.(1)如图 1,为边上一点,为边延长线上一点,且,连接,交于点.① 求证:;② 过点作,垂足为,求证:;(2)如图 2,已知,将沿射线平移,得到△,连接,,请直接写出的最小值.4.(2025 春 青羊区校级期中)•在菱形 ABCD 中,∠ABC=60°,点 P 是射线 BD 上一动点,以 AP为边向右侧作等边△APE,点 E 的位置随点 P 的位置变化而变化.(1)如图 1,当点 E 在菱形 ABCD 内部时,连接 CE,则 BP 与 CE 的数量关系是 ,CE与 AD 的位置关系是 ;(2)如图 2,当点 E 在菱形 ABCD 外部时,连接 CE.求证:CE+PD=BD;(3)如图 3,当点 P 在线段 BD 的延长线上时,连接 BE.若,,求 PD.5.(2025 春 连城县期中)•如图①,点是等边中线上一点,连接,为等边三角形,连接.(1)求证:;(2)如图②,当在线段的延长线上,求证:;(3)如图③,,点是射线的动点,是否其中存在以、、为顶点的菱形,若存在,请直接写出线段的长度(不写过程),若不存在,说明理由.6.(2025 春 思明区校级期中)•如图 1,平面直角坐标系中,点,,点在轴...