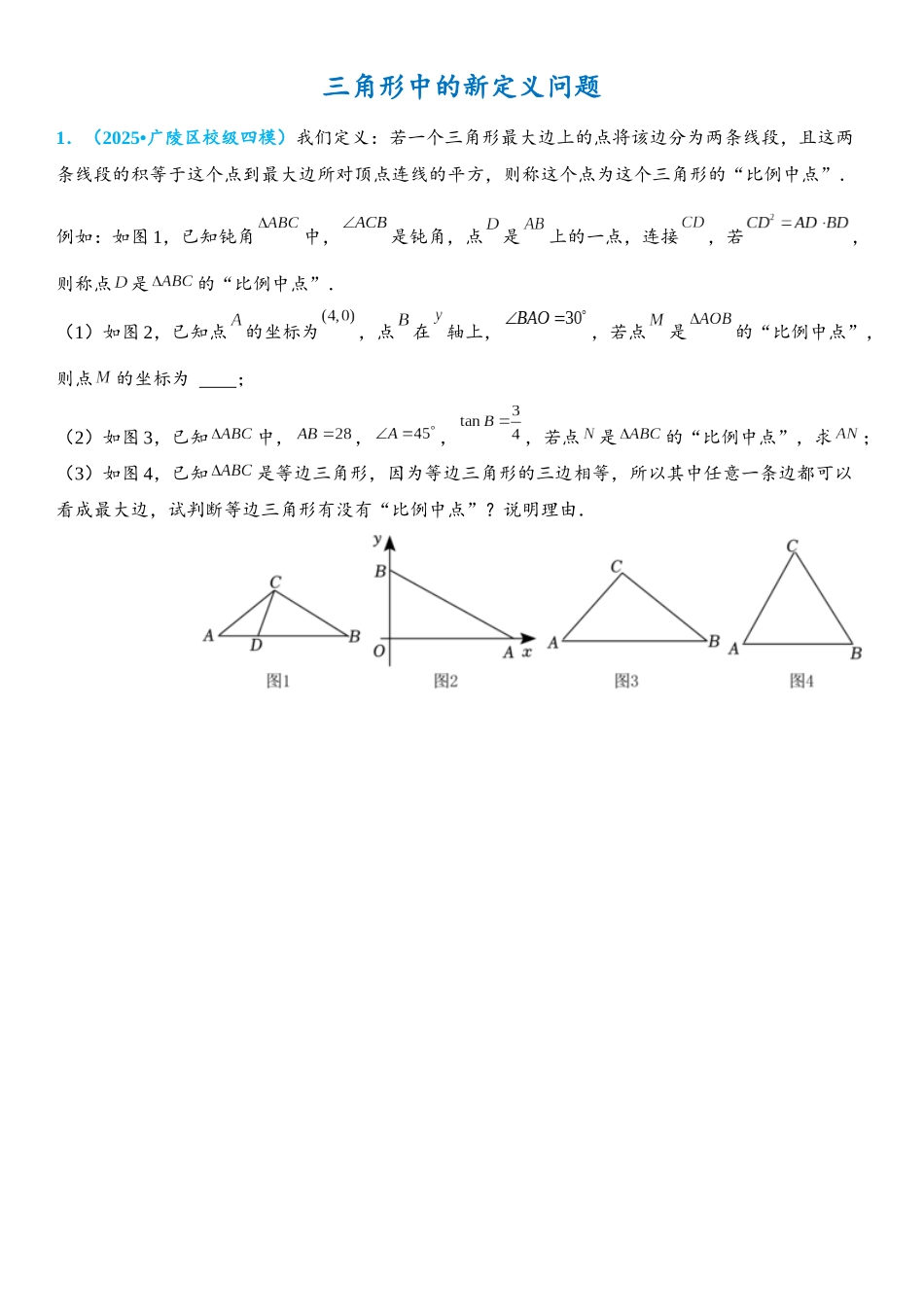
三角形中的新定义问题1.(2025•广陵区校级四模)我们定义:若一个三角形最大边上的点将该边分为两条线段,且这两条线段的积等于这个点到最大边所对顶点连线的平方,则称这个点为这个三角形的“比例中点”.例如:如图 1,已知钝角中,是钝角,点是上的一点,连接,若,则称点是的“比例中点”.(1)如图 2,已知点的坐标为,点在轴上,,若点是的“比例中点”,则点的坐标为 ;(2)如图 3,已知中,,,,若点是的“比例中点”,求;(3)如图 4,已知是等边三角形,因为等边三角形的三边相等,所以其中任意一条边都可以看成最大边,试判断等边三角形有没有“比例中点”?说明理由.2.(2025 秋 泰兴市期中)•我们类比黄金分割点给出如下定义:如图点、、在同一条直线上,,则称点为,的“银杏点”.特别地,若为的中点时,则为,的“银杏点”, 也为,的“银杏点”.(1)已知,点在线段上,若点为,的“银杏点”,则 .(2)如图,为的重心,则下列说法正确的是 (填序号).①为,的“银杏点”;②为,的“银杏点”;③为,的“银杏点”;④为,的“银杏点”.(3)如图,在中,.若,.① 求的长;② 当点在边上,且、、中有一点为其它两点的“银杏点”.点在直线上,且.求的长.3.(2025•任城区三模)我们定义:等腰三角形中底边与腰的比叫做顶角的正对.如图①在中,,顶角的正对记作,这时.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题:(1) .(2) .(3)如图②,已知,其中为锐角,试求的值.4.(2025 秋 鼓楼区校级期末)•定义 1:如图 1,若点在直线 上,在 的同侧有两条以为端点的线段、,满足,则称和关于直线 满足“光学性质”;定义 2:如图 2,在中,的三个顶点、、分别在,、上,若和关于满足“光学性质”, 和关于满足“光学性质”, 和关于满足“光学性质”,则称为的光线三角形.阅读以上定义,并探究问题:在中,,,三个顶点、、分别在、,上.(1)如图 3,若,和关于满足“光学性质”,求的度数;(2)如图 4,在中,作于,以为直径的圆分别交,于点,.① 证明:为的光线三角形;② 证明:的光线三角形是唯一的.5.(2025•柯城区模拟)定义:若三角形的一条边上的高线与这条边相等,则称这个三角形为“等底高三角形”,这条边叫做等底线,这条边上的高叫做等高线.如图:在,于点,且,则为等底高三角形,叫等底线,叫等...