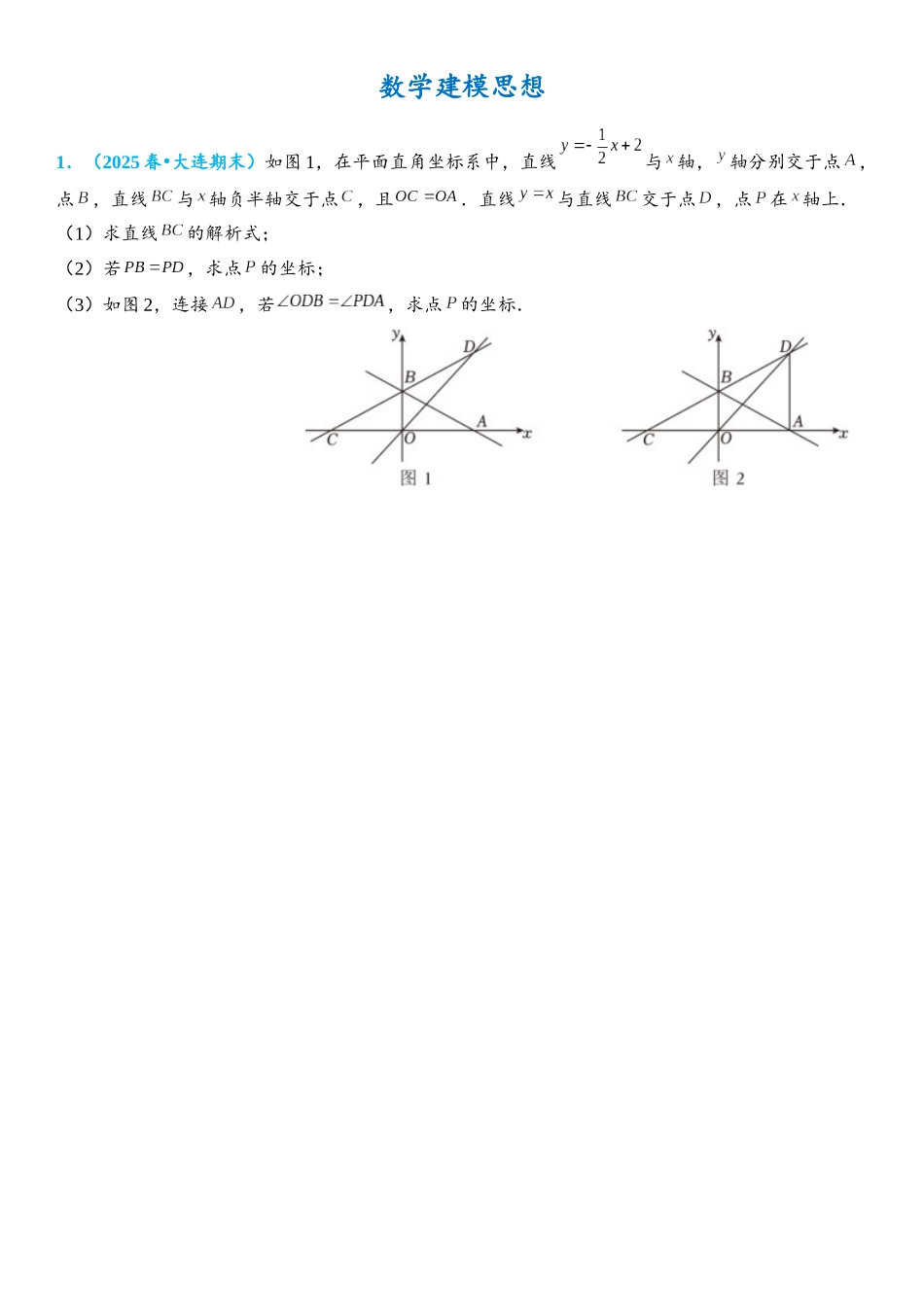
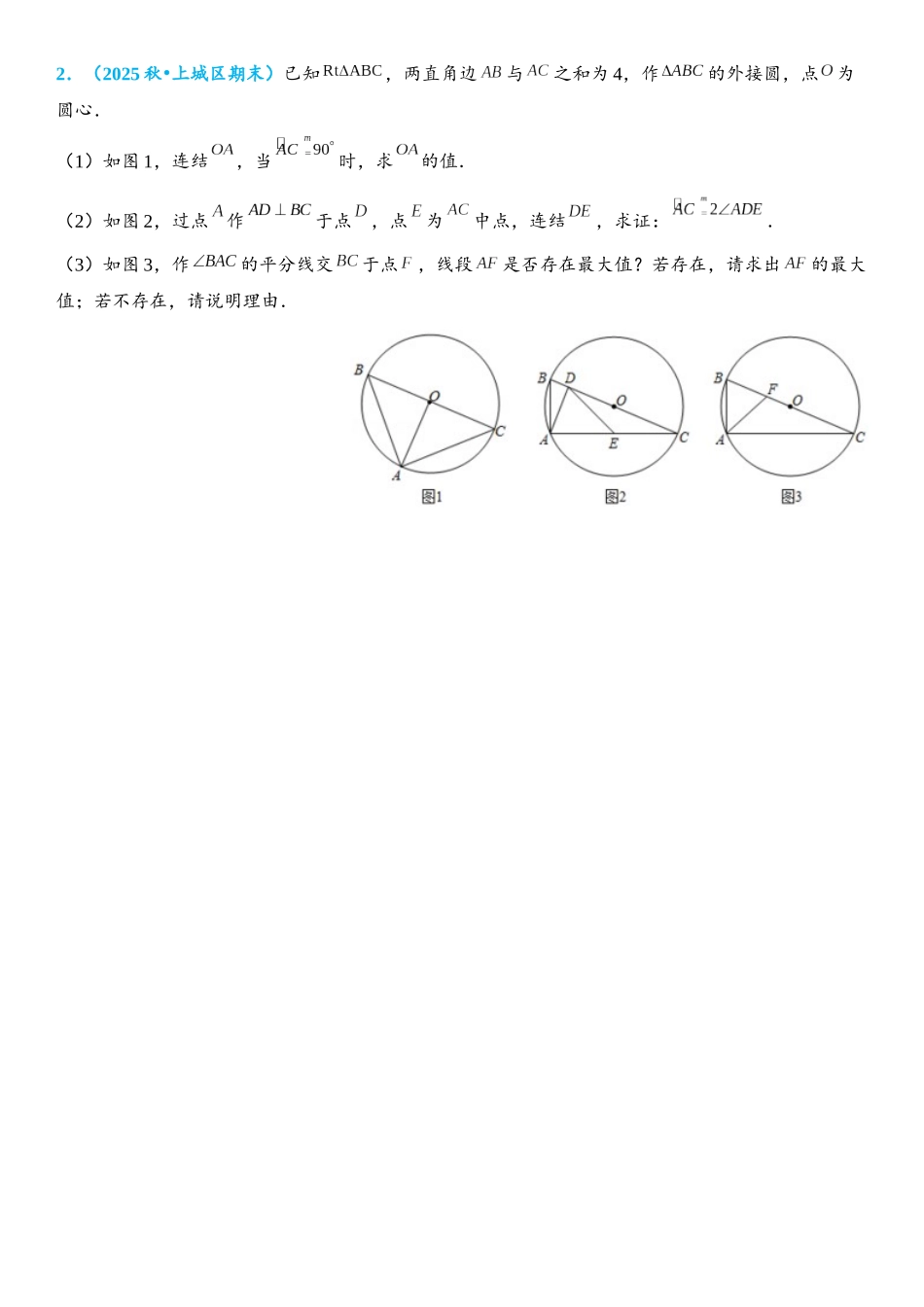
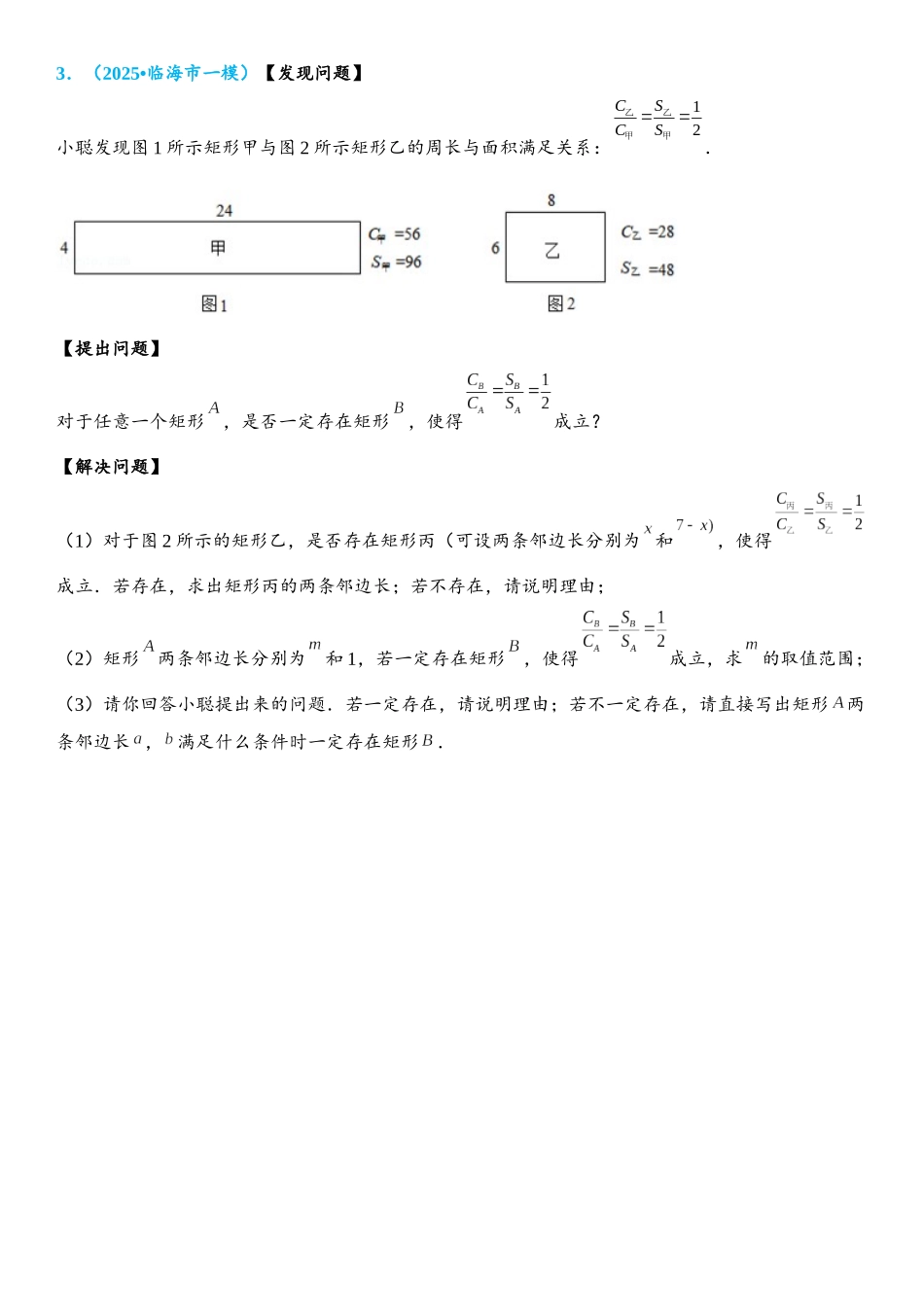
数学建模思想1.(2025 春 大连期末)•如图 1,在平面直角坐标系中,直线与 轴,轴分别交于点,点,直线与 轴负半轴交于点,且.直线与直线交于点,点在 轴上.(1)求直线的解析式;(2)若,求点的坐标;(3)如图 2,连接,若,求点的坐标.2.(2025 秋 上城区期末)•已知,两直角边与之和为 4,作的外接圆,点为圆心.(1)如图 1,连结,当时,求的值.(2)如图 2,过点作于点,点为中点,连结,求证:.(3)如图 3,作的平分线交于点,线段是否存在最大值?若存在,请求出的最大值;若不存在,请说明理由.3.(2025•临海市一模)【发现问题】小聪发现图 1 所示矩形甲与图 2 所示矩形乙的周长与面积满足关系:.【提出问题】对于任意一个矩形,是否一定存在矩形,使得成立?【解决问题】(1)对于图 2 所示的矩形乙,是否存在矩形丙(可设两条邻边长分别为 和,使得成立.若存在,求出矩形丙的两条邻边长;若不存在,请说明理由;(2)矩形两条邻边长分别为和 1,若一定存在矩形,使得成立,求的取值范围;(3)请你回答小聪提出来的问题.若一定存在,请说明理由;若不一定存在,请直接写出矩形两条邻边长 , 满足什么条件时一定存在矩形.4.(2024 秋 汉阳区校级月考)•某商品的进价为每件 40 元,售价为每件 50 元,每个月可卖出 210件;如果每件商品的售价每上涨 1 元,则每个月少卖 10 件(每件售价不能高于 65 元).设每件商品的售价上涨 元为正整数),每个月的销售利润为元.(1)求与 的函数关系式并直接写出自变量 的取值范围.(2)每件商品的售价定为多少元时,每个月的利润恰为 2200 元?(3)根据以上结论,请你直接写出售价在什么范围时,每个月的利润不低于 2200 元?5.(2024•白下区一模)(1)在遇到问题:“钟面上,如果把时针与分针看作是同一平面内的两条线段,在之间,时针与分针重合的时刻是多少?”时,小明尝试运用建立函数关系的方法:① 恰当选取变量 和.小明设 2 点钟之后经过,时针、分针分别与竖轴线(即经过表示“12”和“6”的点的直线,如图所成的角的度数为、;② 确定函数关系.由于时针、分针在单位时间内转动的角度不变,因此既可以直接写出、关于的函数关系式,也可以画出它们的图象.小明选择了后者,画出了图 2;③ 根据题目的要求,利用函数求解.本题中小明认为求出两个图象交点的横坐标就可以解决问题.请你按照小明的思路解决这...