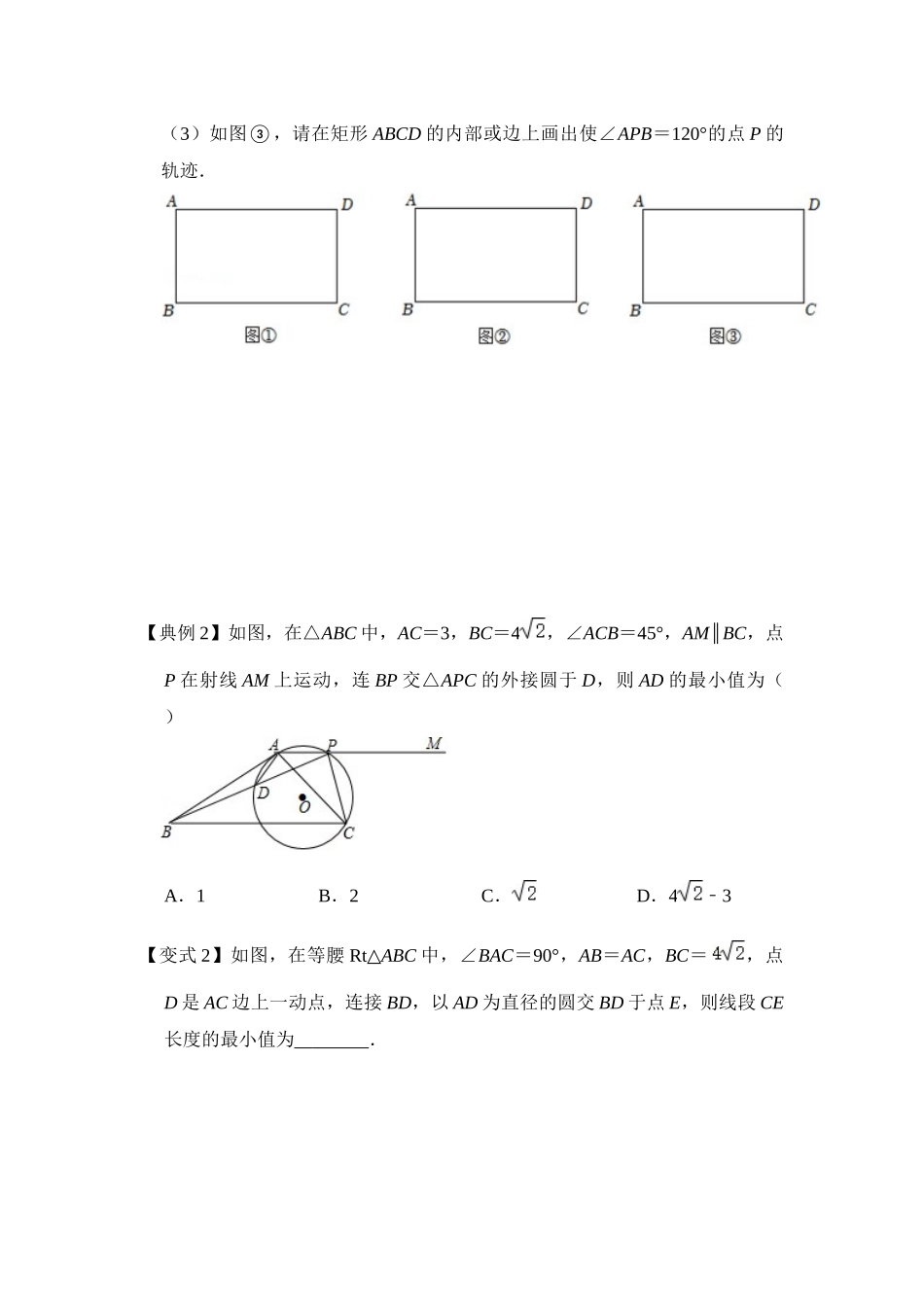
专题 04 定弦定角(知识解读)【专题说明】 定弦定角题型的识别:有一个定弦,一个主动点,一个从动点,定弦所对的张角固定不变。图形中一般求一个从动点到一个定点线段长度最值问题,一般涉及定弦定角最值问题【知识点】若固定线段 AB 所对动角∠P 为定值,则点 P 运动轨迹为过 A、B、P 三点的圆。备注:点 P 在优弧、劣弧上运动皆可。原理:同弧所对的圆周角相等;同弧所对的圆周角等于圆心角的一半。请在上方后面的图形中找到圆心。【方法技巧】解题技巧:构造隐圆定弦定角解决问题的步骤:(1)让动点动一下,观察另一个动点的运动轨迹,发现另一个动点的运动轨迹为一段弧。(2)找不变的张角(这个时候一般是找出张角的补角),(这个补角一般为、)(3)找张角所对的定弦,根据三点确定隐形圆,确定圆心位置(4)计算隐形圆的半径(5)圆心与所求线段上定点的距离可以求出来(6)最小值等于圆心到定点之间的距离减去半径【典例分析】【典例 1】如图,已知矩形 ABCD.(1)如图①,请在矩形 ABCD 的内部或边上画出使∠APB=45°的点 P 的轨迹;(2)如图②,请在矩形 ABCD 的内部或边上画出使∠APB=90°的点 P 的轨迹;(3)如图③,请在矩形 ABCD 的内部或边上画出使∠APB=120°的点 P 的轨迹.【典例 2】如图,在△ABC 中,AC=3,BC=4,∠ACB=45°,AM∥BC,点P 在射线 AM 上运动,连 BP 交△APC 的外接圆于 D,则 AD 的最小值为( )A.1B.2C.D.43﹣【变式 2】如图,在等腰 Rt△ABC 中,∠BAC=90°,AB=AC,BC=,点D 是 AC 边上一动点,连接 BD,以 AD 为直径的圆交 BD 于点 E,则线段 CE长度的最小值为 .【典例 3】如图,⊙O 半径为 6,弦 AB=6,点 P 为优弧 AB 上一动点,AC⊥AP交直线 PB 于点 C,则△ABC 的最大面积是( )A.6B.9C.6D.9【变式 3】如图, ⊙O 的半径为 1,弦 AB=1,点 P 为优弧上一动点 ,AC⊥AP 交直线 PB 于点 C,则△ABC 的最大面积是( )A.B.C.D.【典例 4】如图,A(1,0)、B(3,0),以 AB 为直径作⊙M,射线 OF 交⊙M于 E、F 两点,C 为弧 AB 的中点,D 为 EF 的中点.当射线 OF 绕 O 点旋转时,CD 的最小值为 .【变式 4】(2025•肇源县二模)如图,A(2,0)、B(6,0),以 AB 为直径作⊙M,射线 OF 交⊙M 于 E、F 两点,C 为弧 AB 的中点,D 为 EF 的中点.当射...