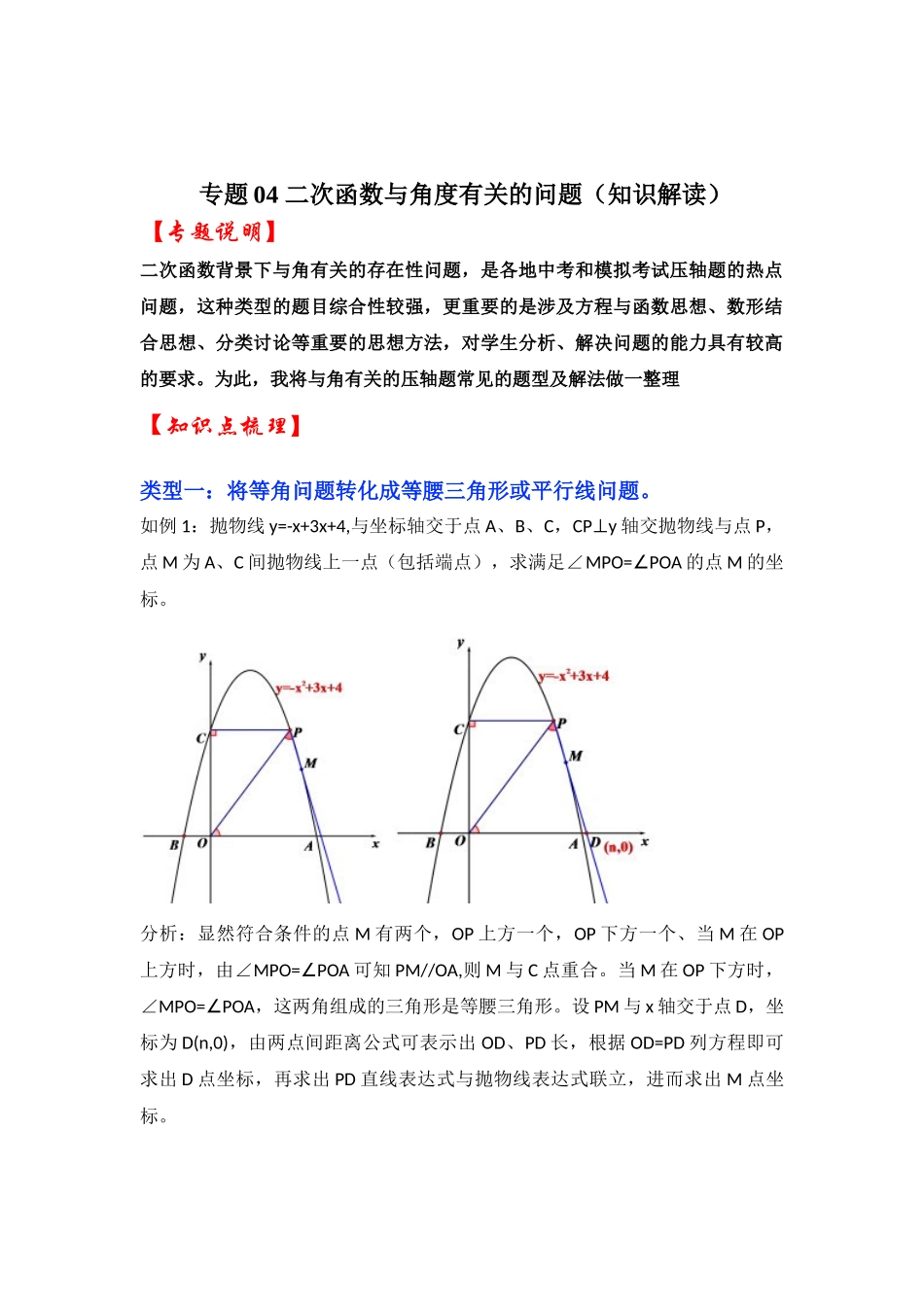
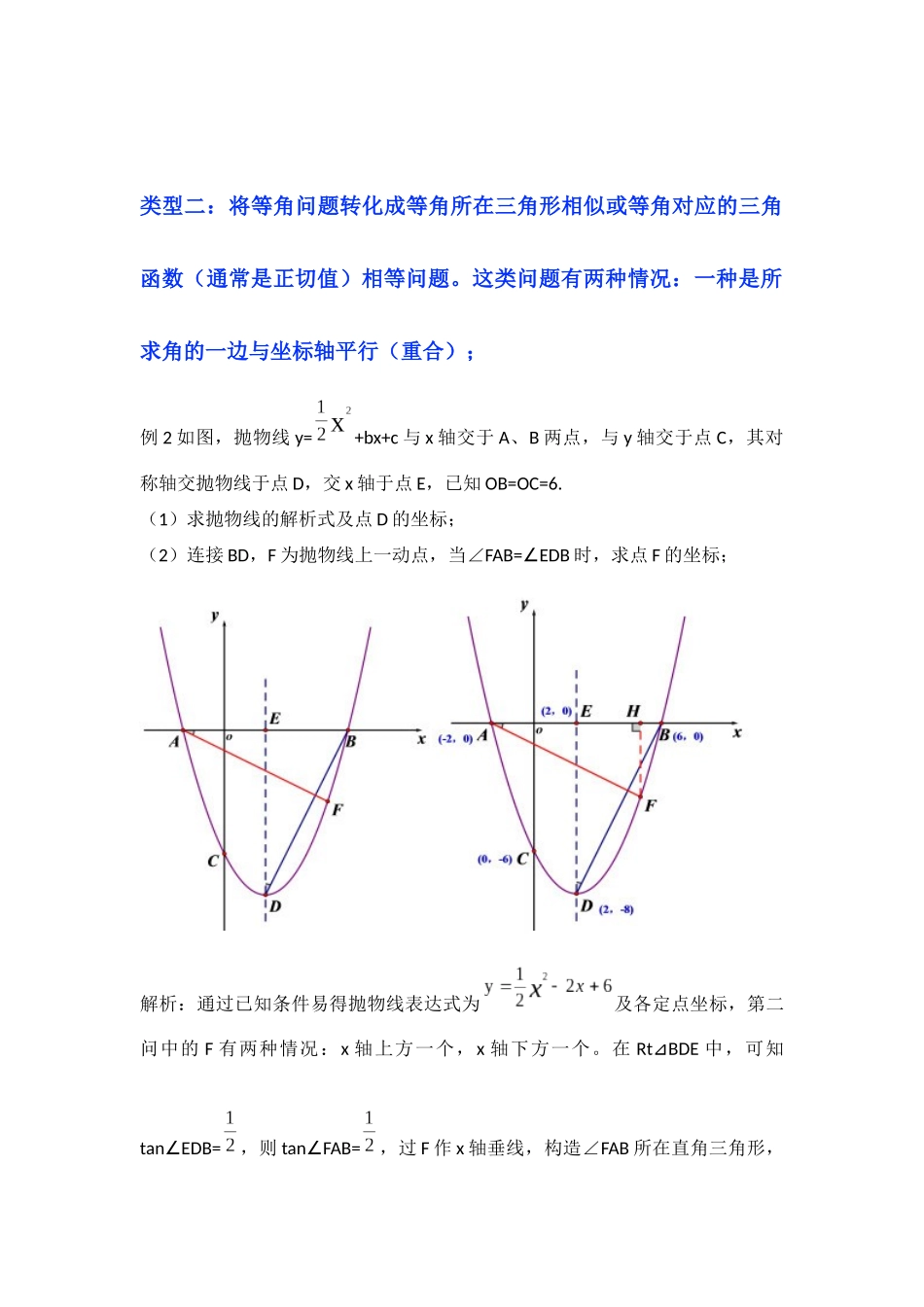
专题 04 二次函数与角度有关的问题(知识解读)【专题说明】二次函数背景下与角有关的存在性问题,是各地中考和模拟考试压轴题的热点问题,这种类型的题目综合性较强,更重要的是涉及方程与函数思想、数形结合思想、分类讨论等重要的思想方法,对学生分析、解决问题的能力具有较高的要求。为此,我将与角有关的压轴题常见的题型及解法做一整理【知识点梳理】类型一:将等角问题转化成等腰三角形或平行线问题。如例 1:抛物线 y=-x+3x+4,与坐标轴交于点 A、B、C,CPy⊥ 轴交抛物线与点 P,点 M 为 A、C 间抛物线上一点(包括端点),求满足∠MPO=POA∠的点 M 的坐标。分析:显然符合条件的点 M 有两个,OP 上方一个,OP 下方一个、当 M 在 OP上方时,由∠MPO=POA∠可知 PM//OA,则 M 与 C 点重合。当 M 在 OP 下方时,∠MPO=POA∠,这两角组成的三角形是等腰三角形。设 PM 与 x 轴交于点 D,坐标为 D(n,0),由两点间距离公式可表示出 OD、PD 长,根据 OD=PD 列方程即可求出 D 点坐标,再求出 PD 直线表达式与抛物线表达式联立,进而求出 M 点坐标。类型二:将等角问题转化成等角所在三角形相似或等角对应的三角函数(通常是正切值)相等问题。这类问题有两种情况:一种是所求角的一边与坐标轴平行(重合);例 2 如图,抛物线 y=+bx+c 与 x 轴交于 A、B 两点,与 y 轴交于点 C,其对称轴交抛物线于点 D,交 x 轴于点 E,已知 OB=OC=6.(1)求抛物线的解析式及点 D 的坐标;(2)连接 BD,F 为抛物线上一动点,当∠FAB=EDB∠时,求点 F 的坐标;解析:通过已知条件易得抛物线表达式为及各定点坐标,第二问中的 F 有两种情况:x 轴上方一个,x 轴下方一个。在 RtBDE⊿中,可知tanEDB=∠,则 tanFAB=∠,过 F 作 x 轴垂线,构造∠FAB 所在直角三角形,接着通过设 F 点坐标,表示 FH 和 AH 长,根据 tanFAB=∠列方程,或利用相似三角形对应边成比例列式,从而求出点 F 坐标,由于表示 FH 时加了绝对值,已经考虑到了上下两种情况,这样两个 F 就都求出来了。还可以从图形的角度发现一对反 8 的相似三角形,推出 AF 与 BD 是垂直关系,进而求出 AF 的直线表达式与抛物线表达式联立求出交点 F 的坐标,这也是不错的方法。另一种是所求角的边不与坐标轴平行。例 3:如图,在平面直角坐标系中,直线 y=x+2 与 x 轴交于点 A,与 y 轴交于点C,...