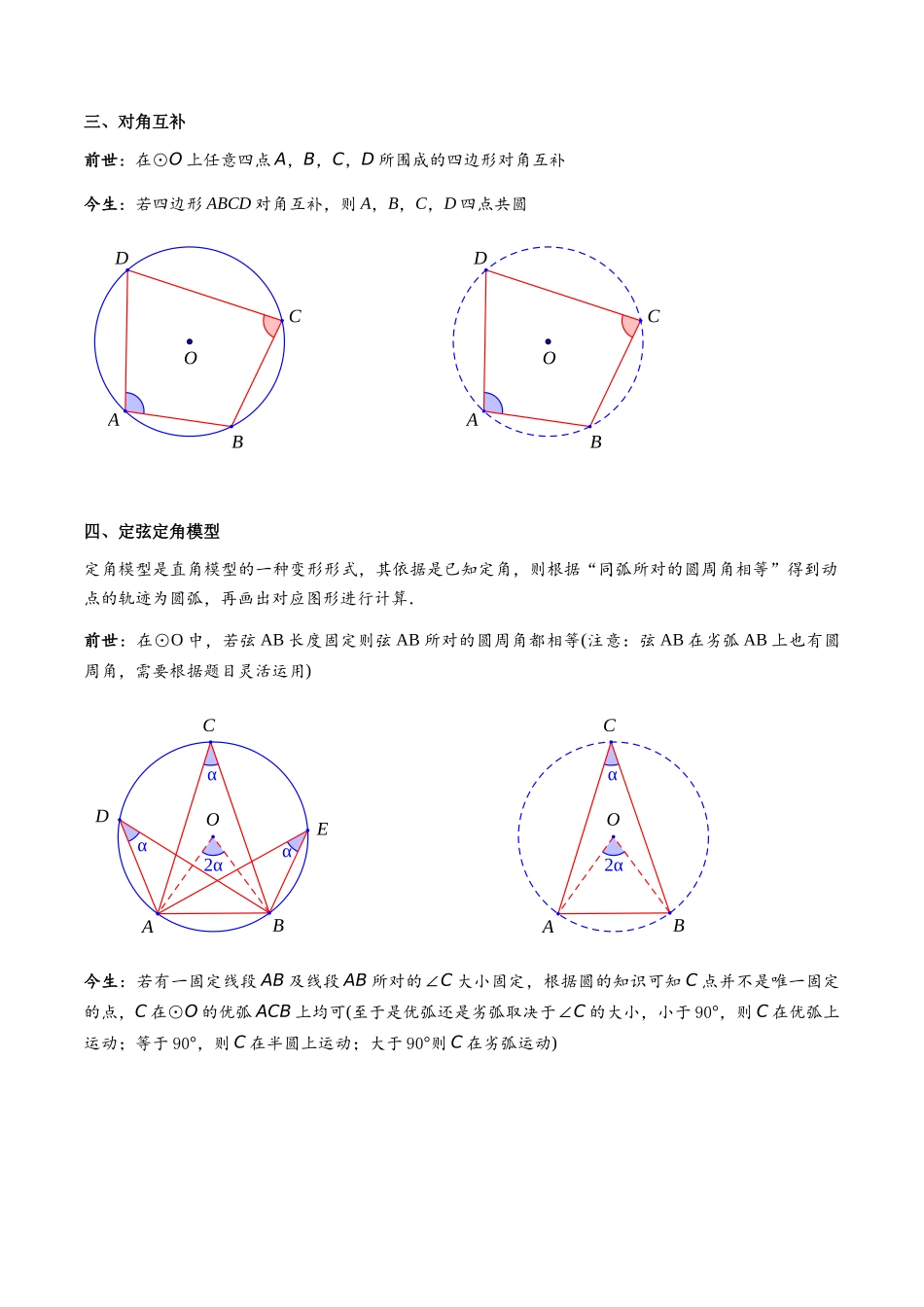
专题 2-3 八种隐圆类最值问题,圆来如此简单 在中考数学中,有一类高频率考题,几乎每年各地都会出现,明明图形中没有出现“圆”,但是解题中必须用到“圆”的知识点,像这样的题我们称之为“隐圆模型”。正所谓:有“圆”千里来相会,无“圆”对面不相逢。“隐圆模型”的题的关键突破口就在于能否看出这个“隐藏圆”。一旦“圆”形毕露,则答案手到擒来!01题型·解读知识点梳理题型一 定点定长得圆2025 年湖北省鄂州市中考数学真题2025·邵阳市中考真题2025·广西南宁市二模2025·辽宁抚顺·中考真题2025·长春·中考真题题型二 直角的对边是直径2025·菏泽市中考真题2025·通辽·中考真题2025·汕头市金平区一模2025·广州市天河区三模2025·成都市成华区二诊题型三 对角互补得圆2025 年·广元市一模题型四 定弦定角得圆2025·成都市新都区二模2025·成都市金牛区二模2025·达州·中考真题题型五 四点共圆题型六 相切时取到最值2025·随州市中考真题2025·江苏无锡·中考真题2025 扬州中考真题题型七 定角定高面积最小、周长最小问题题型八 米勒角(最大张角)模型徐州中考满分·技巧02 知识点梳理一、定点定长得圆在几何图形中,通过折叠、旋转,滑梯模型得到动点的轨迹为绕定点等于定长的圆,从而画出动点轨迹,并进行计算xyCABOM二、直角的对边是直径前世:在⊙O 中,AB 为直径,则始终有 AB 所对的∠C=90°今生:若有 AB 是固定线段,且总有∠ACB=90°,则 C 在以 AB 为直径径的圆上.(此类型本来属于定弦定角,但是因为比较特殊,故单独分为一类)BOACBOAC三、对角互补前世:在⊙O 上任意四点 A,B,C,D 所围成的四边形对角互补今生:若四边形 ABCD 对角互补,则 A,B,C,D 四点共圆OADBCOADBC四、定弦定角模型定角模型是直角模型的一种变形形式,其依据是已知定角,则根据“同弧所对的圆周角相等”得到动点的轨迹为圆弧,再画出对应图形进行计算.前世:在⊙O 中,若弦 AB 长度固定则弦 AB 所对的圆周角都相等(注意:弦 AB 在劣弧 AB 上也有圆周角,需要根据题目灵活运用)2ααααOABCDEα2αOABC今生:若有一固定线段 AB 及线段 AB 所对的∠C 大小固定,根据圆的知识可知 C 点并不是唯一固定的点,C 在⊙O 的优弧 ACB 上均可(至于是优弧还是劣弧取决于∠C 的大小,小于 90°,则 C 在优弧上运动;等于 90°,则 C 在半圆上运动;大于 90°则 C 在劣弧运动)五、四点共...