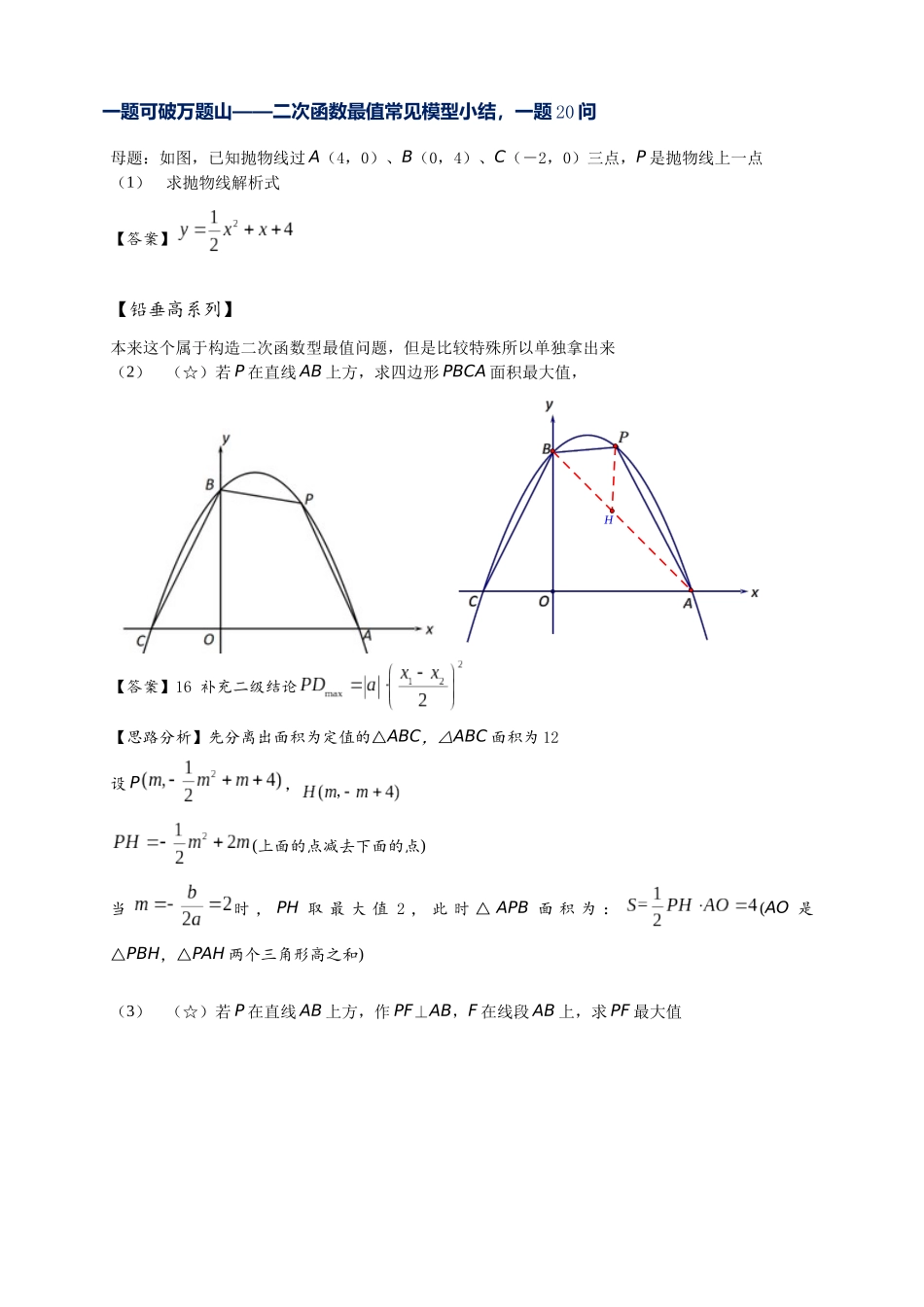
专题 2-7 二次函数中的最值问题一题可破万题山——二次函数最值常见模型小结,一题 20 问题型一 【铅垂高系列】2025·四川凉山·中考真题2025·天津·中考真题2025·湖北襄阳·统考中考真题2025·湖南娄底·中考真题2025·湖南中考真题2025·青海西宁·中考真题2025·四川广安·中考真题2025·湖南永州·中考真题2025·四川广元·中考真题题型二 【线段和差最值篇】2025·湖南张家界中考真题2025·山东淄博·统考中考真题2025·四川遂宁中考真题题型三 【构造二次函数模型求最值】2025·山东东营·中考真题2025·四川巴中·中考真题2025·湖南张家界中考真题2025·山东聊城·中考真题2025·湖北襄阳中考真题2025·湖北荆州中考真题2025·江苏连云港中考真题2025·湖南岳阳·中考真题2025·宁夏·中考真题2025·湖北襄阳中考真题题型四 【加权线段最值】2025·四川内江·中考真题2025·黑龙江绥化·中考真题题型五 【几何构造最值篇】2025·天津·统考中考真题一题可破万题山——二次函数最值常见模型小结,一题 20 问母题:如图,已知抛物线过 A(4,0)、B(0,4)、C(-2,0)三点,P 是抛物线上一点(1)求抛物线解析式 【答案】【铅垂高系列】本来这个属于构造二次函数型最值问题,但是比较特殊所以单独拿出来(2)(☆)若 P 在直线 AB 上方,求四边形 PBCA 面积最大值, •H【答案】16 补充二级结论【思路分析】先分离出面积为定值的△ABC,△ABC 面积为 12设 P,(上面的点减去下面的点)当时 , PH 取 最 大 值 2 , 此 时 △ APB 面 积 为 :(AO 是△PBH,△PAH 两个三角形高之和)(3)(☆)若 P 在直线 AB 上方,作 PF⊥AB,F 在线段 AB 上,求 PF 最大值xyFBOCAPH【答案】【思路分析】过 P 作 PH 平行 y 轴,H 在 AB 上导角可知△PFH~△AOB 为等腰直角三角形,PH 取最大时,PF 也取到最大(4)(★)若 P 在直线 AB 上方,作 PF⊥AB,交线段 AB 于 F,作 PE∥y 轴交 AB 于 E,求△PEF 周长和面积的最大值xyEFBOCAPxy45°45°EFBOCAP【答案】2+2和 1【思路分析】△PEF 形状固定,(5)若 P 在直线 AB 上方,连接 OP,交 AB 于 D,求的最大值xyDBOCAPxyHDBOCAP【答案】【思路分析】化斜为直,平行线,构造 8 字相似转换(6)(★☆)若 P 在直线 AB 上方,连接 CP,交 AB 于 D,△PDA 面积为 S1,△CDA 面积为S2,求的最小值xy...