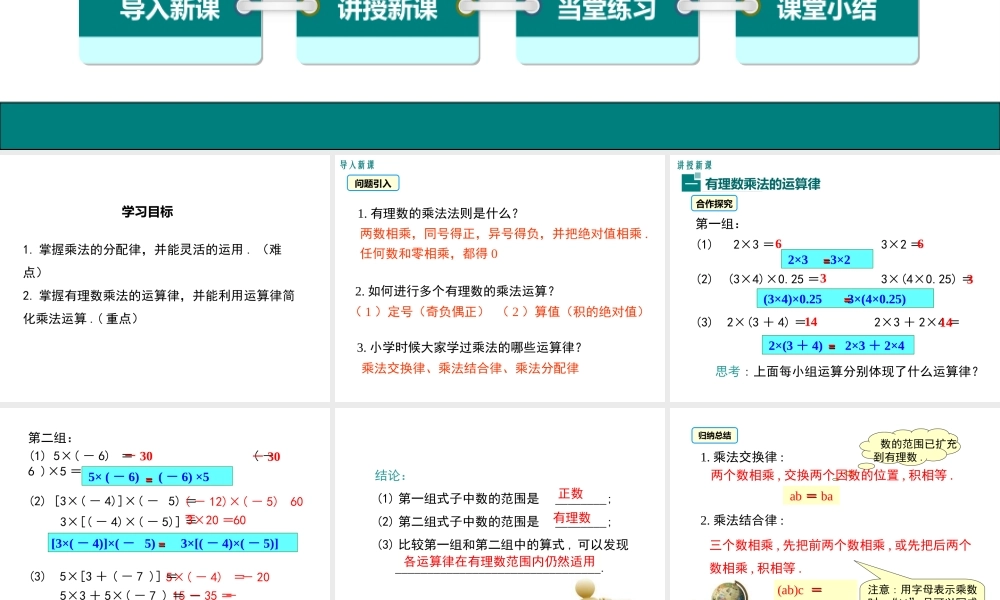
导入新课讲授新课当堂练习课堂小结1.4.1 有理数的乘法第一章 有理数第 2 课时 有理数乘法的运算律及运用1.4 有理数的乘除法七年级数学上( RJ ) 教学课件学习目标1. 掌握乘法的分配律,并能灵活的运用 . (难点)2. 掌握有理数乘法的运算律,并能利用运算律简化乘法运算 .( 重点)导入新课问题引入1. 有理数的乘法法则是什么?3. 小学时候大家学过乘法的哪些运算律?两数相乘,同号得正,异号得负,并把绝对值相乘 .任何数和零相乘,都得 0 乘法交换律、乘法结合律、乘法分配律2. 如何进行多个有理数的乘法运算?( 1 )定号(奇负偶正) ( 2 )算值(积的绝对值)第一组:(2) (3×4)×0.25 = 3×(4×0.25) = (3) 2×(3 + 4) = 2×3 + 2×4 =(1) 2×3 = 3×2 =思考 : 上面每小组运算分别体现了什么运算律? 2×3 3×2 (3×4)×0.25 3×(4×0.25) 2×(3 + 4) 2×3 + 2×466331414======讲授新课有理数乘法的运算律一合作探究5×( - 4) =15 -- 35 =第二组:(2) [3×( - 4)]×( - 5) = 3×[( - 4)×( - 5)] = (3) 5×[3 + ( - 7 )] = 5×3 + 5×( - 7 ) =(1) 5×( - 6) = ( -6 )×5 =- 30- 306060- 20-20 5× ( - 6) ( - 6) ×5[3×( - 4)]×( - 5) 3×[( - 4)×( - 5)]5×[3 + ( - 7 )] 5×3 + 5×( - 7 ) ======( - 12)×( - 5) =3×20 = 结论: (1) 第一组式子中数的范围是 ________; (2) 第二组式子中数的范围是 ________; (3) 比较第一组和第二组中的算式 , 可以发现 ________________________________.正数有理数各运算律在有理数范围内仍然适用两个数相乘 , 交换两个因数的位置 , 积相等 .ab == ba三个数相乘 , 先把前两个数相乘 , 或先把后两个数相乘 , 积相等 .(ab)c == a(bc) 1. 乘法交换律 :2. 乘法结合律 : 数的范围已扩充到有理数 .注意 : 用字母表示乘数时 ,“×” 号可以写成“ ·” 或省略 , 如a×b 可以写成 a·b 或ab.归纳总结一个数同两个数的和相乘 , 等于把这个数分别同这两个数相乘 , 再把积相加 .3. 乘法分配律:a(b +c)ab +ac==根据乘法交换律和结合律可以推出:三个以上有理数相乘 , 可以任意交换因数的位置 , 也可先把其中的几个数相乘 .根...