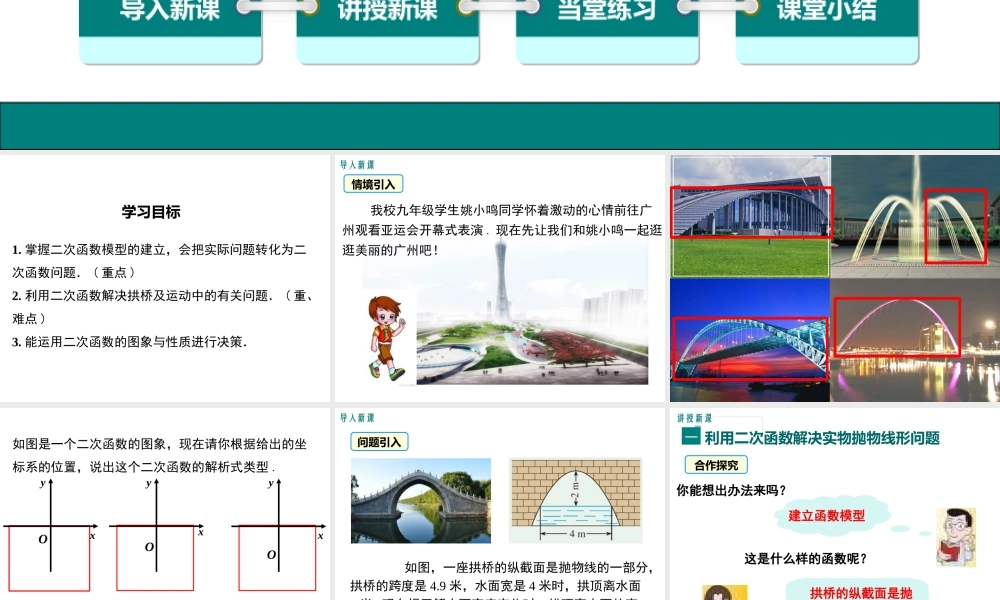
22.3 实际问题与二次函数第二十二章 二次函数导入新课讲授新课当堂练习课堂小结第 3 课时 拱桥问题和运动中的抛物线九年级数学上( RJ ) 教学课件学习目标1. 掌握二次函数模型的建立,会把实际问题转化为二次函数问题. ( 重点 )2. 利用二次函数解决拱桥及运动中的有关问题. ( 重、难点 )3. 能运用二次函数的图象与性质进行决策.导入新课情境引入 我校九年级学生姚小鸣同学怀着激动的心情前往广州观看亚运会开幕式表演 . 现在先让我们和姚小鸣一起逛逛美丽的广州吧!如图是一个二次函数的图象,现在请你根据给出的坐标系的位置,说出这个二次函数的解析式类型 .xyxyxy( 1 ) y=ax2( 2 ) y=ax2+k( 3 ) y=a(x-h)2+k( 4 ) y=ax2+bx+cOOO导入新课问题引入 如图,一座拱桥的纵截面是抛物线的一部分,拱桥的跨度是 4.9 米,水面宽是 4 米时,拱顶离水面2 米 . 现在想了解水面宽度变化时,拱顶离水面的高度怎样变化.你能想出办法来吗?讲授新课利用二次函数解决实物抛物线形问题一建立函数模型这是什么样的函数呢? 拱桥的纵截面是抛物线,所以应当是个二次函数你能想出办法来吗?合作探究怎样建立直角坐标系比较简单呢?以拱顶为原点,抛物线的对称轴为 y 轴,建立直角坐标系,如图.从图看出,什么形式的二次函数,它的图象是这条抛物线呢?由于顶点坐标系是( 0.0 ),因此这个二次函数的形式为2yax-2-421-2-1A如何确定 a 是多少?已知水面宽 4 米时,拱顶离水面高 2 米,因此点 A( 2 , -2 )在抛物线上,由此得出因此, ,其中 | x |是水面宽度的一半, y 是拱顶离水面高度的相反数,这样我们就可以了解到水面宽度变化时,拱顶离水面高度怎样变化.212yx222a g12a 解得由于拱桥的跨度为 4.9 米,因此自变量 x 的取值范围是:水面宽 3m 时 从而因此拱顶离水面高 1.125m32x 21391.125228y2.452.45x 现在你能求出水面宽 3 米时,拱顶离水面高多少米吗?我们来比较一下( 0 , 0 )( 4 , 0 )( 2 , 2 )( -2 , -2 ) ( 2 , -2 )( 0 , 0 )( -2 , 0 )( 2 , 0 )( 0 , 2 )( -4 , 0 )( 0 , 0 )( -2 , 2 )谁最合适yyyyooooxxxx知识要点建立二次函数模型解决实际问题的基本步骤是什么?实际问题建立二次函数模型利用二次函数的...