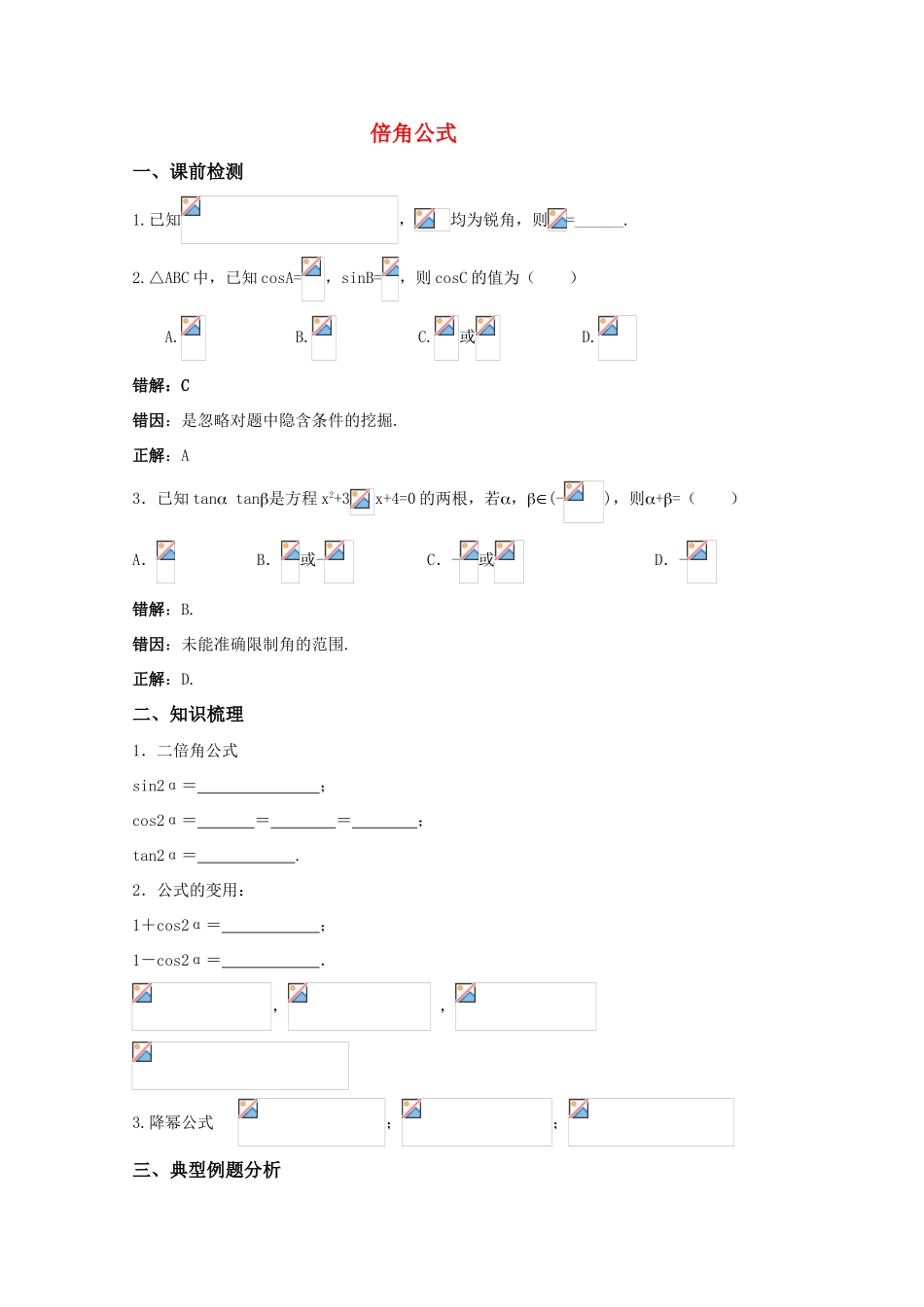
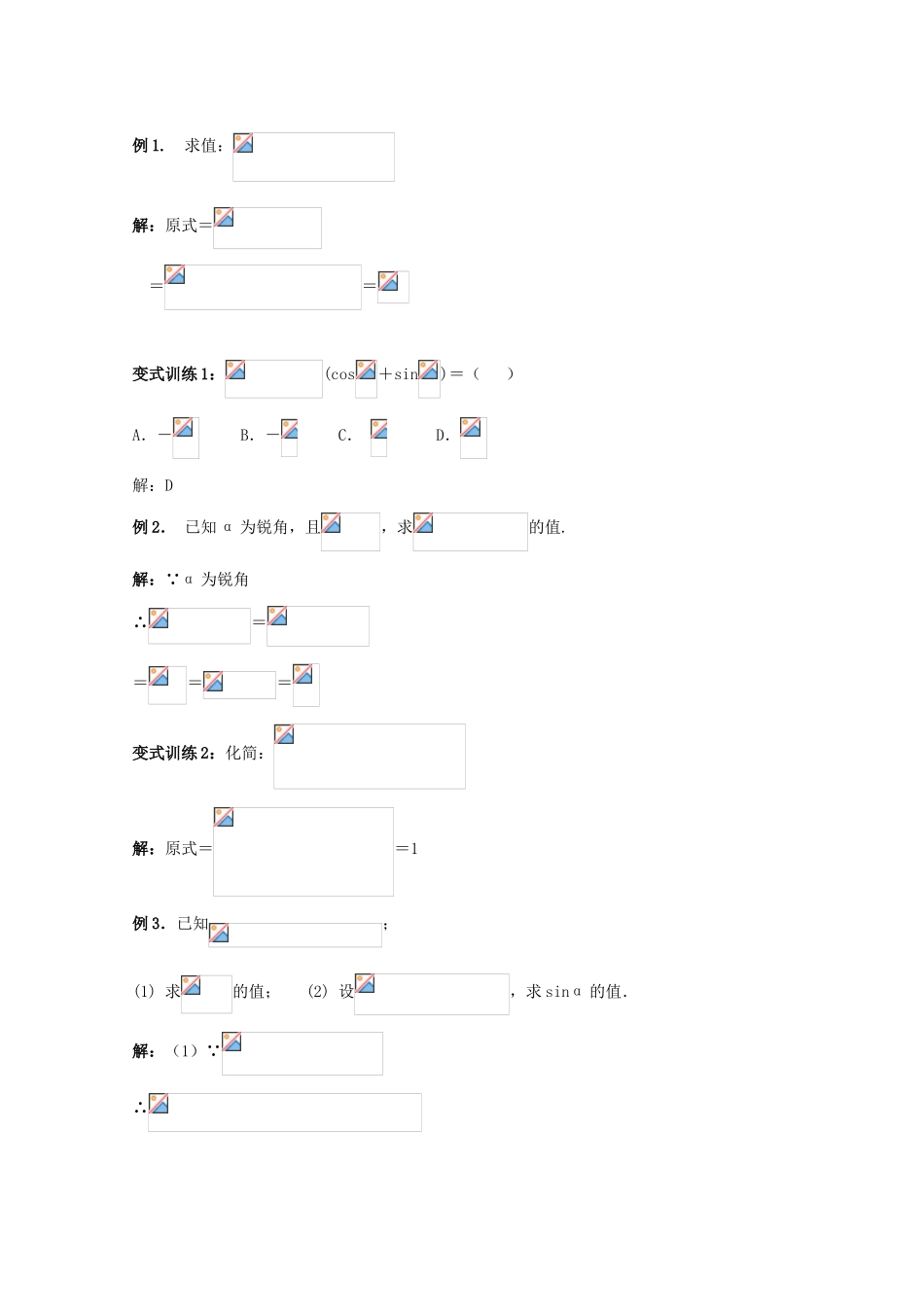
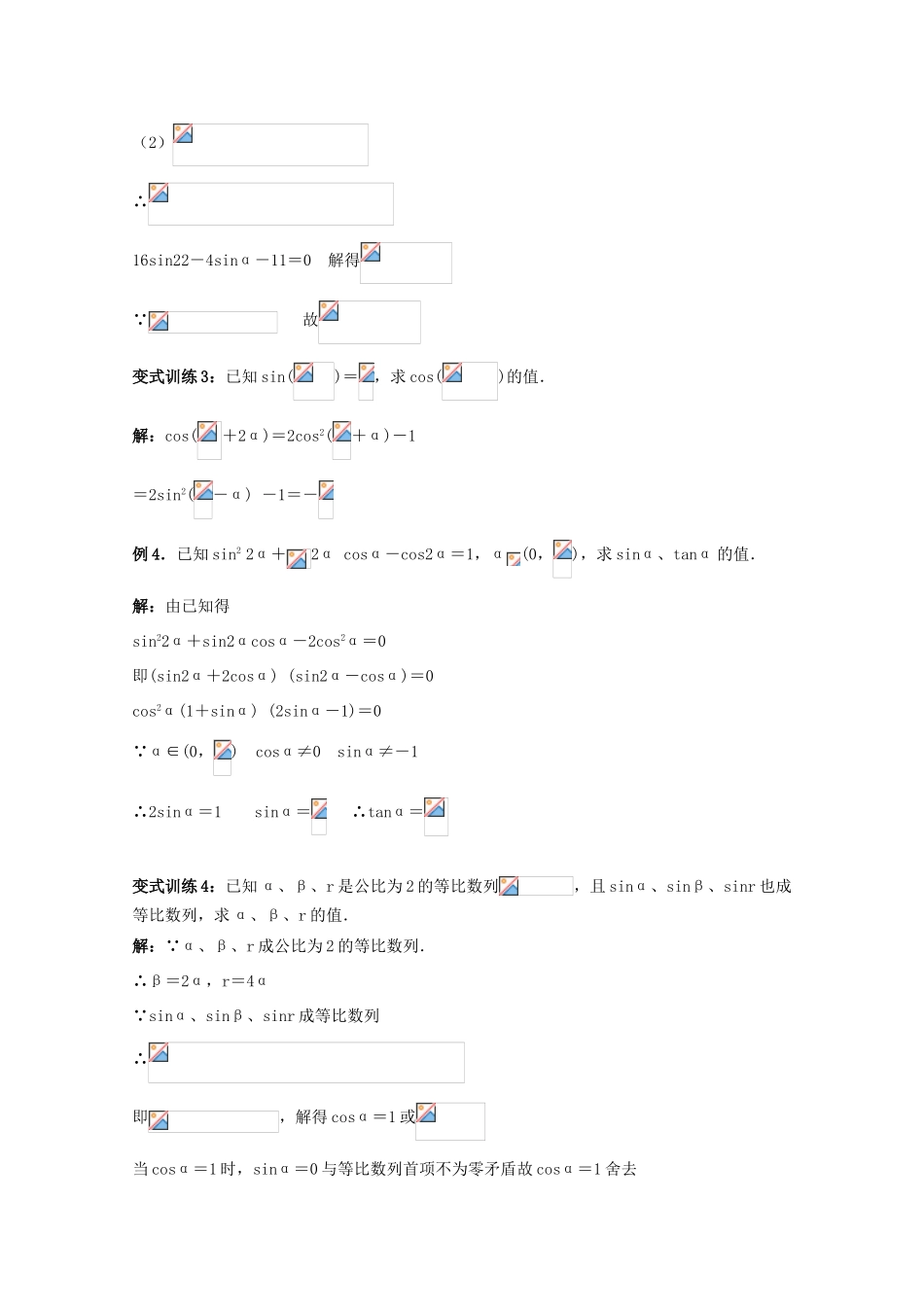
倍角公式一、课前检测1.已知,均为锐角,则=______.2.△ABC 中,已知 cosA=,sinB=,则 cosC 的值为( ) A. B. C.或 D.错解:C错因:是忽略对题中隐含条件的挖掘.正解:A3.已知 tan tan是方程 x2+3x+4=0 的两根,若,(-),则+=( )A. B.或- C.-或 D.-错解:B.错因:未能准确限制角的范围.正解:D.二、知识梳理1.二倍角公式sin2α= ;cos2α= = = ;tan2α= .2.公式的变用:1+cos2α= ;1-cos2α= ., ,3.降幂公式 ;;三、典型例题分析例 1. 求值:解:原式= ==变式训练 1:(cos+sin)=( )A.- B.- C. D. 解:D例 2. 已知 α 为锐角,且,求的值. 解:∵α 为锐角∴====变式训练 2:化简:解:原式==1例 3.已知;(1) 求的值; (2) 设,求 sinα 的值.解:(1)∵∴(2)∴16sin22-4sinα-11=0 解得∵ 故变式训练 3:已知 sin()=,求 cos()的值.解:cos(+2α)=2cos2(+α)-1=2sin2(-α) -1=-例 4.已知 sin2 2α+2α cosα-cos2α=1,α(0,),求 sinα、tanα 的值.解:由已知得sin22α+sin2αcosα-2cos2α=0即(sin2α+2cosα) (sin2α-cosα)=0cos2α(1+sinα) (2sinα-1)=0∵α∈(0,) cosα≠0 sinα≠-1∴2sinα=1 sinα= ∴tanα=变式训练 4:已知 α、β、r 是公比为 2 的等比数列,且 sinα、sinβ、sinr 也成等比数列,求 α、β、r 的值.解:∵α、β、r 成公比为 2 的等比数列.∴β=2α,r=4α∵sinα、sinβ、sinr 成等比数列∴即,解得 cosα=1 或当 cosα=1 时,sinα=0 与等比数列首项不为零矛盾故 cosα=1 舍去当时,∵2∈[0,2π] ∴或∴或四、归纳与总结(以学生为主,师生共同完成)1.二倍角公式是和角公式的特殊情况,在学习时要注意它们之间的联系;2.要理解二倍角的相对性,能根据公式的特点进行灵活应用(正用、逆用、变形用).3.对三角函数式的变形有以下常用的方法:① 降次(常用降次公式)② 消元(化同名或同角的三角函数)③ 消去常数“1”或用“1”替换④ 角的范围的确定