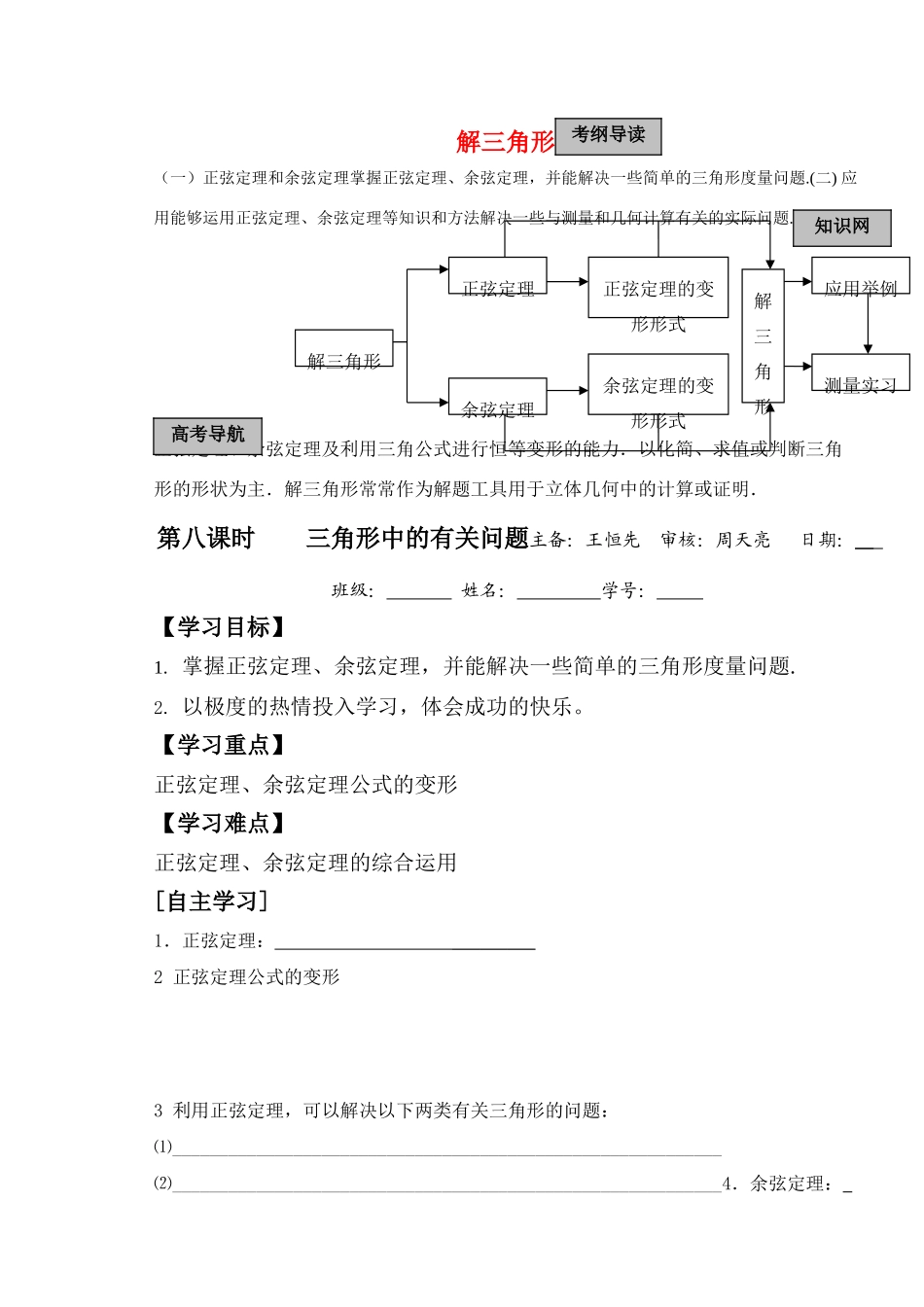
解三角形(一)正弦定理和余弦定理掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题.(二) 应用能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题.正弦定理、余弦定理及利用三角公式进行恒等变形的能力.以化简、求值或判断三角形的形状为主.解三角形常常作为解题工具用于立体几何中的计算或证明.第八课时 三角形中的有关问题主备:王恒先 审核:周天亮 日期: 班级: 姓名: 学号: 【学习目标】1. 掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题.2. 以极度的热情投入学习,体会成功的快乐。【学习重点】正弦定理、余弦定理公式的变形【学习难点】正弦定理、余弦定理的综合运用[自主学习]1.正弦定理: _________ 2 正弦定理公式的变形3 利用正弦定理,可以解决以下两类有关三角形的问题:⑴___________________________________________________________⑵___________________________________________________________4.余弦定理: 解三角形正弦定理余弦定理正弦定理的变形形式余弦定理的变形形式解三角形应用举例测量实习知识网络考纲导读高考导航5 余弦定理公式的变形6 利用余弦定理,可以解决以下两类有关三角形的问题.⑴___________________________________________________________⑵___________________________________________________________7.三角形的面积公式: [典型例析]例 1. (1)在△ABC 中,若 sinA=2sinB cos C, sin2A=sin2B+sin2C,试判断△ABC 的形状.(2)在△ABC 中,sinA=,判断这个三角形的形状例 2. 已知△ABC 中,2(sin2A-sin2C)=(a-b)sinB,△ABC 外接圆半径为.(1)求∠C;(2)求△ABC 面积的最大值.变式训练: 在△ABC 中,所对的边分别为,,且(1)求的值;(2)若,求的最大值;例 3.如图,已知△ABC 是边长为 1 的正三角形,M、N 分别是边 AB、AC 上的点,线段MN 经过△ABC 的中心 G.设∠MGA=().(1)试将△AGM、△AGN 的面积(分别记为 S1与 S2)表示为的函数;(2)求 y=的最大值与最小值.[当堂检测]1 在△ABC 中,= .2 的内角 A、B、C 的对边分别为 a、b、c,若 a、b、c 成等比数列,且,则__________________ 3 在△ABC 中,已知,,则的值为_________________4 若钝角三角形三边长为、、,则 的取值范围是 [学后反思]____________________________________________________ _______ _____________________________________________________________