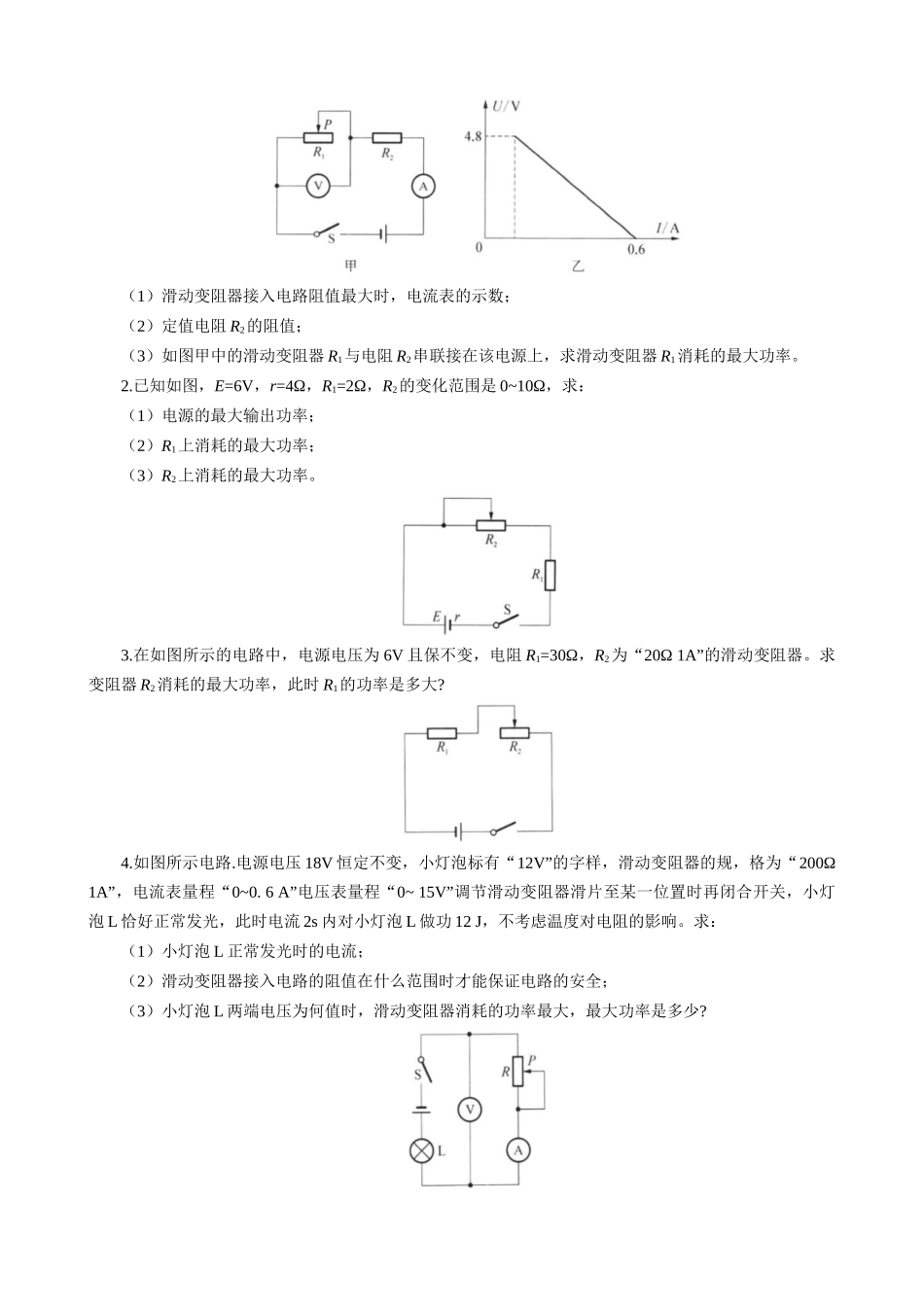
滑动变阻器的最大功率一、要点解析1.定值电阻的功率:P=I2R1,R1不变,所以电流 I 越大,功率越大,即当滑动变阻器阻值最小时,定值电阻的电功率最大。2.滑动变阻器的功率:P=I2R2,因为电流 I 随着 R2的变化而变化,所以我们要将公式变形:,由基本不等式可知:当且仅当 R2=R1时,“=”成立,即当 R2=R1时,滑动变阻器的电功率有最大值:。我们将 P-R2图像画出,如图 2 所示,可知当 R2越接近 R1时,电功率越大。 图 1 图 2 图 3 3.总功率 P,R1的功率 P1,R2的功率 P2随电流 I 的变化情况:P=IU(U 为电源电压,恒定,所以图像为正比例函数);P1=I2R1(图像为过原点的二次函数,且开口向上);P2=U2I=(U-U1)I =UI-I2R1=-R1(图像为二次函数,开口向下,且有最大值)。三者随电流 I 变化的图像如图 3 所示,其中甲为 P-I 图,乙为 P1-I 图,丙为 P2-I 图。二、典例引领例 1.实验小组的同学设计了如图 a 所示的电路,已知电源电压不变,滑动变阻器 R 为“20Ω 2A”,闭合开关 S,调节滑动变阻器滑片 P 的位置,根据电路中电压表和电流表的数据描绘了如图 b 所示的两条 U-I 图线。其中利用电压表 V1和电流表 A 的数据描绘出甲图线,利用电压表 V2和电流表 A 的数据描绘出乙图线。求:(1)定值电阻 R2的阻值;(2)电源电压的大小及定值电阻 R1的阻值;(3)R 消耗的最大功率。解析:(1)图乙是 R2的伏安特性曲线,则:(2)图甲是 V1,即 U2+Up=U-IR1,斜率是与 U 轴的交点为电源电压,即 U=1.5 V(3)当R=R1+R2时,滑动变阻器上的电功率最大:例 2.(多选)某同学将一 直流电源的总功率 PE、输出功率 PR和电源内部的发热功率 Pr,随电流 I变化的图线画在同一坐标系内,如右图所示,根据图线可知( )A.反映 Pr变化的图线是 c B.电源电动势为 8 VC.电源内阻为 2Ω D.当电流为 0.5 A 时,外电路的电阻为 6 Ω解析:Pr=I2r 为二次函数图像即图线 c,故 A 正确,代入图线上的点可以求得 r=2Ω,故 C 正确;PE=UI,电源电压不变为正比例函数图像即图线 a,代入图线上的点可以求得 U=4V,故 B 错;,故 D 正确;选 ACD。三、针对演练1.如图甲,滑动变阻器上标有“40Ω 1A”字样,移动滑片 P,电流表与电压表示数的变化图像如图乙所示。(电源电压恒定)求:(1)滑动变阻器接入电路阻值最大时,电流表的示数;(2)定值电阻 R2的阻值;...