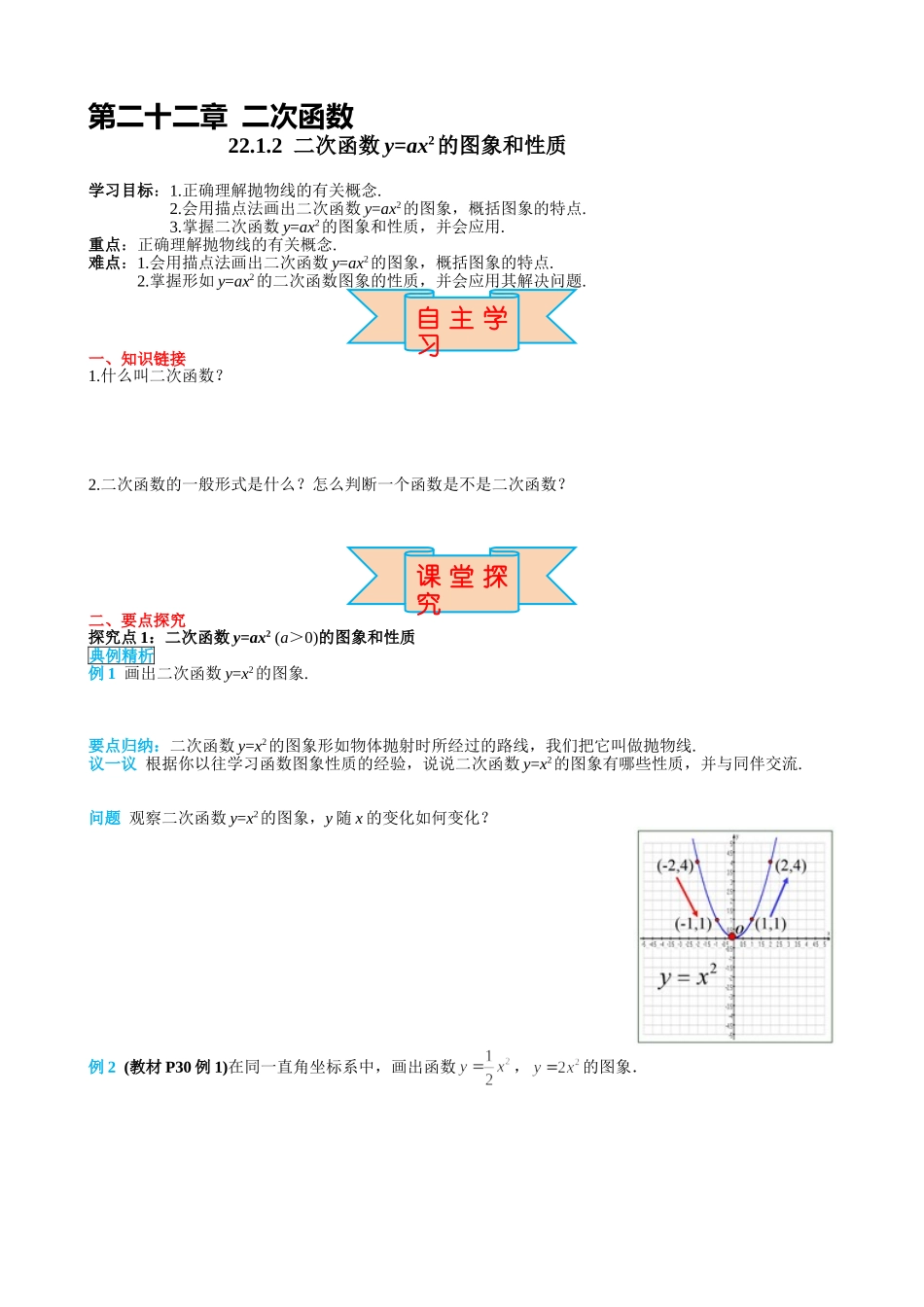
第二十二章 二次函数22.1.2 二次函数 y=ax2的图象和性质学习目标:1.正确理解抛物线的有关概念.2.会用描点法画出二次函数 y=ax2的图象,概括图象的特点. 3.掌握二次函数 y=ax2的图象和性质,并会应用.重点:正确理解抛物线的有关概念.难点:1.会用描点法画出二次函数 y=ax2的图象,概括图象的特点.2.掌握形如 y=ax2的二次函数图象的性质,并会应用其解决问题.一、知识链接1.什么叫二次函数? 2.二次函数的一般形式是什么?怎么判断一个函数是不是二次函数?二、要点探究探究点 1:二次函数 y=ax2 (a>0)的图象和性质典例精析例 1 画出二次函数 y=x2的图象.要点归纳:二次函数 y=x2的图象形如物体抛射时所经过的路线,我们把它叫做抛物线.议一议 根据你以往学习函数图象性质的经验,说说二次函数 y=x2的图象有哪些性质,并与同伴交流.问题 观察二次函数 y=x2的图象,y 随 x 的变化如何变化?例 2 (教材 P30 例 1)在同一直角坐标系中,画出函数,的图象.自 主 学习课 堂 探究思考(1) 函数,的图象与函数 y=x2的图象相比,有什么共同点和不同点?(2) 当 a>0 时,二次函数 y = ax2的图象有什么特点?要点归纳:对于抛物线 y = ax2 (a>0),抛物线开口向上,对称轴是 y 轴,顶点是原点,顶点是抛物线的最低点,a 越大,抛物线的开口越小.探究点 2:二次函数 y=ax2 (a<0)的图象和性质合作探究在同一直角坐标系中,画出函数,,的图象.思考(1) 观察函数,,的图象,思考这些抛物线有什么共同点和不同点?(2) 当 a<0 时,二次函数 y = ax2的图象有什么特点?要点归纳:对于抛物线 y = ax2 (a<0),抛物线开口向下,对称轴是 y 轴,顶点是原点,顶点是抛物线的最高点,a 越小,抛物线的开口越小.问题 观察二次函数 y=-x2的图象,y 随 x 的变化如何变化?交流讨论:抛物线 y=ax2与 y=-ax2(a>0)的关系是什么?练一练1.函数的图象的开口 ,对称轴是 ,顶点是 ;2.函数的图象的开口 ,对称轴是 ,顶点是 ,顶点是抛物线的最 点;3.函数的图象的开口 ,对称轴是 , 顶点是 ,顶点是抛物线的最 点; 4.函数的图象的开口 ,对称轴是 ,顶点是 . 例 3 已知二次函数 y=x2.(1) 判断点 A(2,4)在二次函数图象上吗?(2) 请分别写出点 A 关于 x 轴的对称点 B 的坐标,关于 y 轴的对称点 C 的坐标,关于原点 O 的对称点 D 的坐标;(3) 点 B、C、...