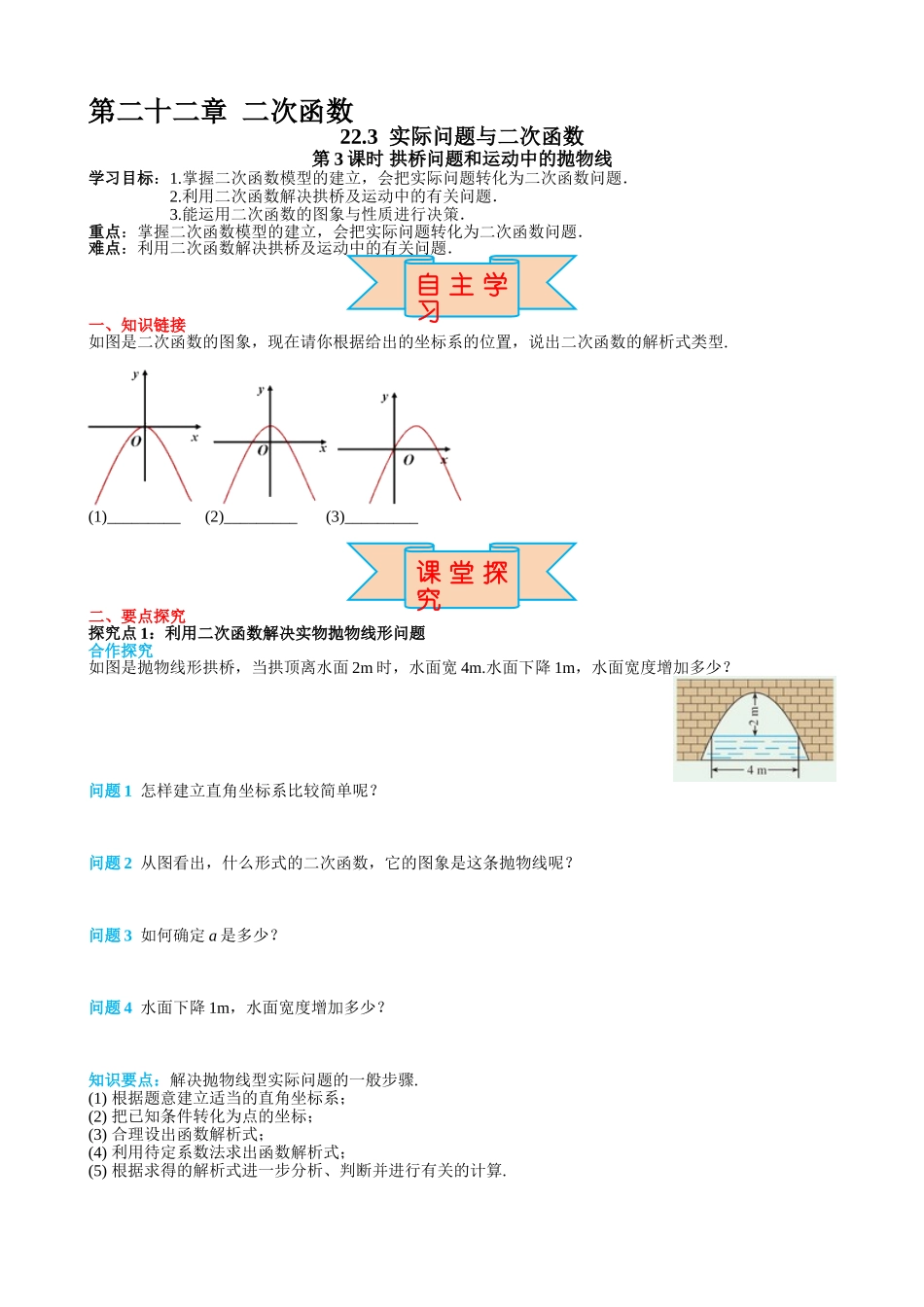
第二十二章 二次函数22.3 实际问题与二次函数第 3 课时 拱桥问题和运动中的抛物线 学习目标:1.掌握二次函数模型的建立,会把实际问题转化为二次函数问题.2.利用二次函数解决拱桥及运动中的有关问题.3.能运用二次函数的图象与性质进行决策.重点:掌握二次函数模型的建立,会把实际问题转化为二次函数问题.难点:利用二次函数解决拱桥及运动中的有关问题.一、知识链接如图是二次函数的图象,现在请你根据给出的坐标系的位置,说出二次函数的解析式类型.(1)_________ (2)_________ (3)_________二、要点探究探究点 1:利用二次函数解决实物抛物线形问题合作探究 如图是抛物线形拱桥,当拱顶离水面 2m 时,水面宽 4m.水面下降 1m,水面宽度增加多少?问题 1 怎样建立直角坐标系比较简单呢?问题 2 从图看出,什么形式的二次函数,它的图象是这条抛物线呢?问题 3 如何确定 a 是多少?问题 4 水面下降 1m,水面宽度增加多少?知识要点:解决抛物线型实际问题的一般步骤.(1) 根据题意建立适当的直角坐标系;(2) 把已知条件转化为点的坐标;(3) 合理设出函数解析式;(4) 利用待定系数法求出函数解析式;(5) 根据求得的解析式进一步分析、判断并进行有关的计算.自 主 学习课 堂 探究典例精析例 1 如图,隧道的截面由抛物线和长方形构成,长方形 OABC 的长是 12m,宽是 4m,按照图中所示的平面直角坐标系,抛物线可以用 y=﹣x2+2x+c 表示.(1)请写出该抛物线的函数关系式;(2)一辆货运汽车载一长方体集装箱后高为 6m,宽为 4m,如果隧道内设双向行车道,那么这辆货车能否安全通过?(3)在抛物线形拱壁上需要安装两排灯,使它们离地面的高度相等.如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?变式 如图所示,施工队要修建一个横断面为抛物线的公路隧道,OM 宽度为 16 米,其顶点 P 到 OM 的距离为 8 米.(1)请建立适当的平面直角坐标系,并求出这条抛物线的函数解析式;(2)隧道下的公路是双向行车道(正中间是一条宽 1 米的隔离带),其中的一条行车道能否行驶宽3.5 米、高 5.8 米的特种车辆?请通过计算说明.探究点 2:利用二次函数解决运动中抛物线型问题例 2 某广场喷泉的喷嘴安装在平地上.有一喷嘴喷出的水流呈抛物线状,喷出的水流高度 y(m)与喷出水流喷嘴的水平距离 x(m)之间满足(1)喷嘴能喷出水流的最大高度是多少?(2)喷嘴喷出水流...