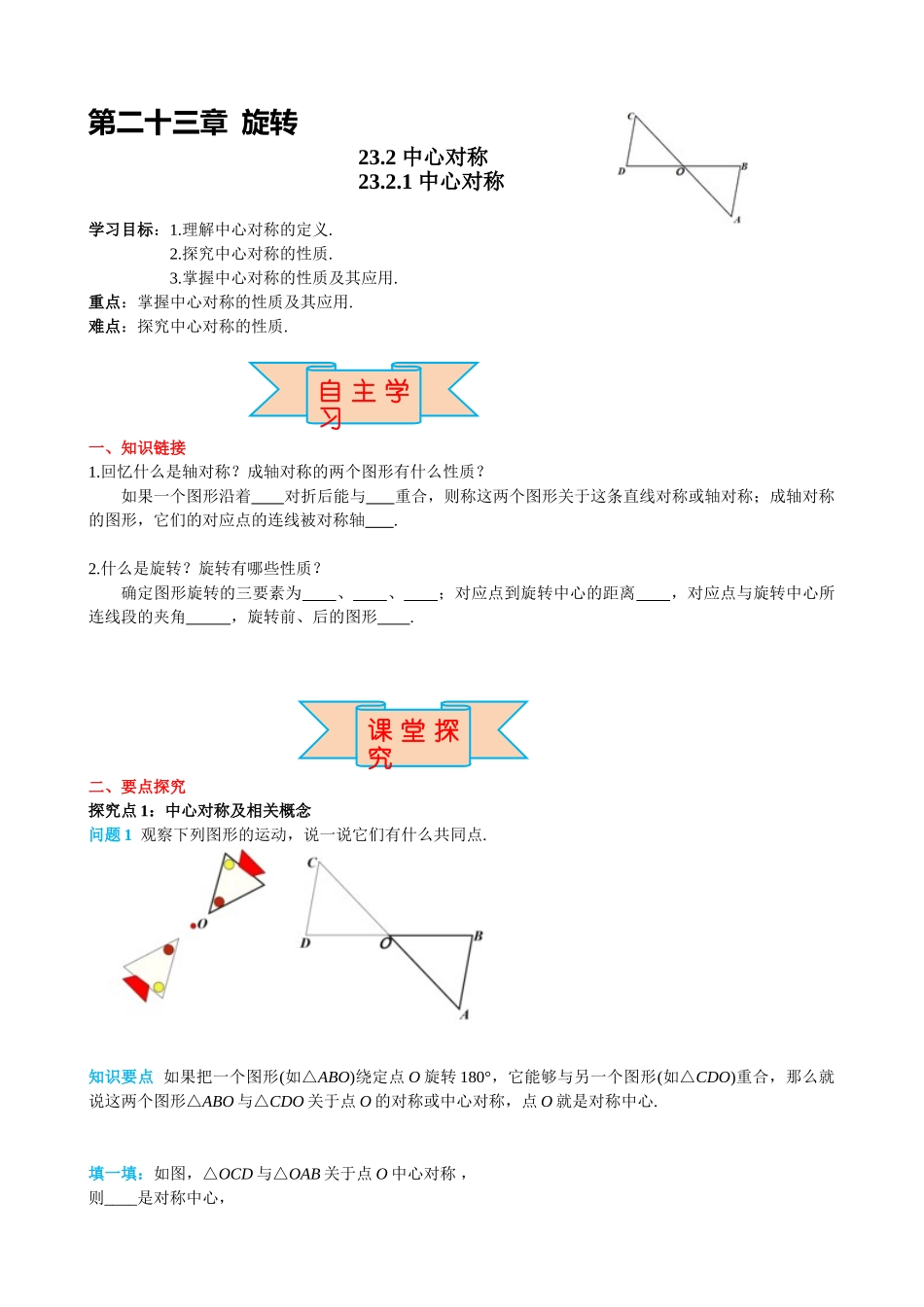
第二十三章 旋转23.2 中心对称23.2.1 中心对称学习目标:1.理解中心对称的定义.2.探究中心对称的性质.3.掌握中心对称的性质及其应用.重点:掌握中心对称的性质及其应用.难点:探究中心对称的性质.一、知识链接1.回忆什么是轴对称?成轴对称的两个图形有什么性质?如果一个图形沿着 对折后能与 重合,则称这两个图形关于这条直线对称或轴对称;成轴对称的图形,它们的对应点的连线被对称轴 .2.什么是旋转?旋转有哪些性质?确定图形旋转的三要素为 、 、 ;对应点到旋转中心的距离 ,对应点与旋转中心所连线段的夹角 ,旋转前、后的图形 .二、要点探究探究点 1:中心对称及相关概念问题 1 观察下列图形的运动,说一说它们有什么共同点. 知识要点 如果把一个图形(如△ABO)绕定点 O 旋转 180°,它能够与另一个图形(如△CDO)重合,那么就说这两个图形△ABO 与△CDO 关于点 O 的对称或中心对称,点 O 就是对称中心.填一填:如图,△OCD 与△OAB 关于点 O 中心对称 ,则____是对称中心, 自 主 学习课 堂 探究点 A 与_____是对称点, 点 B 与____是对称点.典例精析例 1 下列五组图形中,左边的图形与右边的图形成中心对称的有( )A.1 组 B.2 组 C.3 组 D.4 组 方法总结:判断两个图形是否成中心对称,就是看其中一个图形绕某一点旋转 180°后能否与另一个图形重合.要点归纳:1.中心对称是一种特殊的旋转,其旋转角是 180 °.2.中心对称是两个图形之间一种特殊的位置关系.3.成中心对称是两个图形只有一个对称中心,对称中心可能在图形的外部、内部或图形上,当对称点一定在对称中心两侧或与对称中心重合.探究点 2:中心对称的性质问题 2 如图,旋转三角尺,画出△ABC 关于点 O 中心对称的△A′B′C′ . 找一找 下图中△A′B′C′与△ABC 关于点 O 是成中心对称,你能从图中找到哪些等量关系?知识要点 中心对称的性质:1.成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分.(即对称点与对称中心三点共线)2.中心对称的两个图形是全等形.例 2 如图①,△ABC 与△A′B′C′关于点 O 成中心对称,则下列结论不成立的是( )A.点 A 与点 A′是对称点 B.BO=B′O C.AB=A′B′ D.∠ACB=∠C′A′B′ 图① 图②变式 如图②,已知△AOB 与△DOC 成中心对称,△AOB 的面积是 12,AB=3,则△DOC 中 CD 边上的高为________.方法总结:成中心对称...