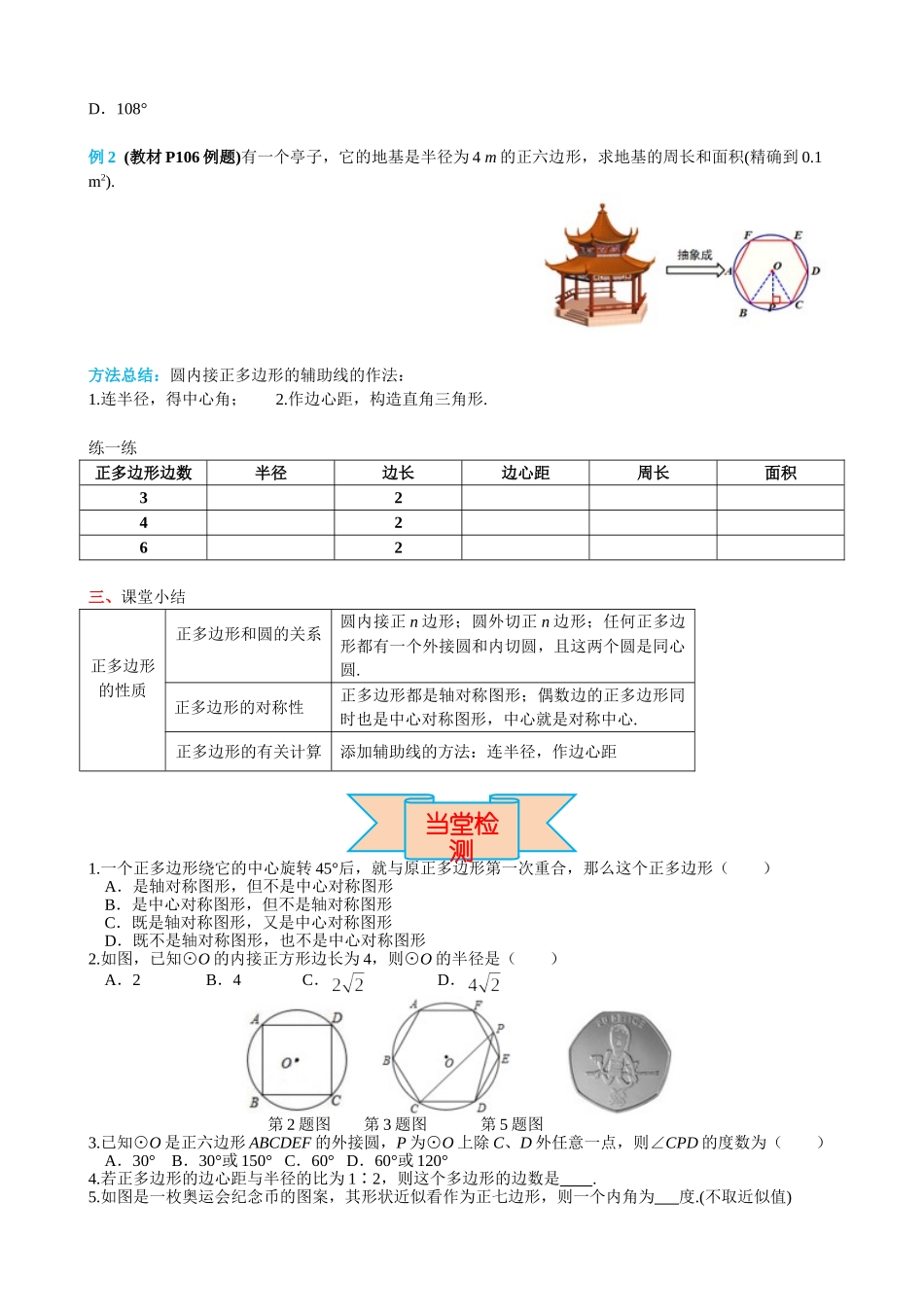
第二十四章 圆24.3 正多边形和圆学习目标:1.了解正多边形和圆的有关概念.2.理解并掌握正多边形半径、中心角、边心距、边长之间的关系. 3.会应用正多边形和圆的有关知识解决实际问题. 重点:理解并掌握正多边形半径、中心角、边心距、边长之间的关系. 难点:会应用正多边形和圆的有关知识解决实际问题. 一、知识链接观察下列各图形,并度量各图形的边长和角度,你有什么发现? 二、要点探究探究点 1:正多边形的对称性问题 1 什么叫做正多边形? 问题 2 矩形是正多边形吗?为什么?菱形是正多边形吗?为什么?问题 3 正三角形、正四边形、正五边形、正六边形都是轴对称图形吗?都是中心对称图形吗?要点归纳:正 n 边形都是轴对称图形,都有 n 条对称轴,只有边数为偶数的正多边形才是中心对称图形.探究点 2:正多边形的有关概念及性质问题 1 怎样把一个圆进行四等分?问题 2 依次连接各等分点,得到一个什么图形?探究归纳把⊙O 进行 5 等分,依次连接各等分点得到五边形 ABCDE .(1)填空:自 主 学习课 堂 探究①_______=______;②_______=______;③ ∠A_____∠E.(2)这个五边形 ABCDE 是正五边形吗?简单说说理由.要点归纳:像上面这样,只要把一个圆分成相等的一些弧,就可以作出这个圆的正多边形,这个圆就是这个正多形的外接圆,这个正多边形也称为这个圆的内接正多边形.问题 3 以正四边形为例,根据对称轴的性质,你能得出什么结论?想一想 所有的正多边形是不是也都有一个外接圆和一个内切圆?要点归纳:正多边形的外接圆和内切圆的公共圆心,叫做正多边形的中心,外接圆的半径叫做正多边形的半径,内切圆的半径叫做正多边形的边心距,正多边形每一条边所对的圆心角,叫做正多边形的中心角,正多边形的每个中心角都等于.练一练 完成下面表格:正多边形边数内角中心角外角346n探究点 3:正多边形的有关计算探究归纳 如图,已知半径为 4 的圆内接正六边形 ABCDEF:① 它的中心角等于 度 ;②OC BC (填>、<或=);③△OBC 是 三角形; ④ 圆内接正六边形的面积是△OBC 面积的 倍.⑤ 圆内接正 n 边形面积公式: .典例精析例 1 如图,正五边形 ABCDE 内接于⊙O,则∠ADE 的度数是 ( )A.60° B.45° C. 36° D. 30° 变式题 如图,圆内接正五边形 ABCDE 中,对角线 AD 和 CE 相交于点 P,则∠APE 的度数是( )A.36° B.60° C.72° D.108° ...