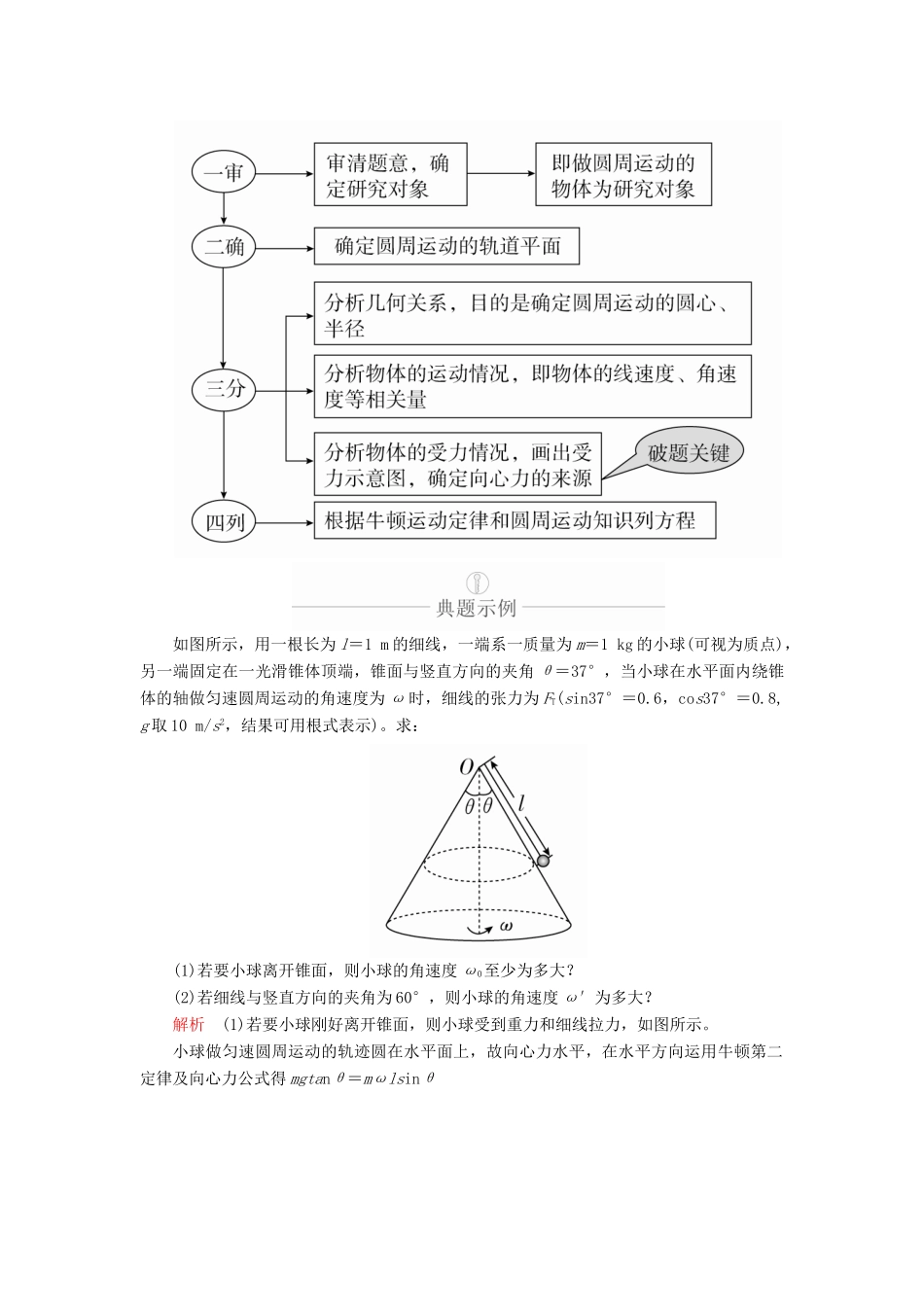
第 20 讲 水平面内的圆周运动考点一 圆锥摆类圆周运动1.向心力的来源向心力是按力的作用效果命名的,可以是重力、弹力、摩擦力等各种力,也可以是几个力的合力或某个力的分力,因此在受力分析中要避免再另外添加一个向心力。2.几种典型运动模型运动模型向心力的来源图示飞机水平转弯火车转弯圆锥摆飞车走壁汽车在倾斜路面转弯3.“一、二、三、四”求解圆周运动问题如图所示,用一根长为 l=1 m 的细线,一端系一质量为 m=1 kg 的小球(可视为质点),另一端固定在一光滑锥体顶端,锥面与竖直方向的夹角 θ=37°,当小球在水平面内绕锥体的轴做匀速圆周运动的角速度为 ω 时,细线的张力为 FT(sin37°=0.6,cos37°=0.8, g 取 10 m/s2,结果可用根式表示)。求:(1)若要小球离开锥面,则小球的角速度 ω0至少为多大?(2)若细线与竖直方向的夹角为 60°,则小球的角速度 ω′为多大?解析 (1)若要小球刚好离开锥面,则小球受到重力和细线拉力,如图所示。小球做匀速圆周运动的轨迹圆在水平面上,故向心力水平,在水平方向运用牛顿第二定律及向心力公式得 mgtanθ=mωlsinθ解得 ω=即 ω0= = rad/s。(2)同理,当细线与竖直方向成 60°角时,由牛顿第二定律及向心力公式得 mgtanα=mω′2lsinα解得 ω′2=即 ω′= =2 rad/s。答案 (1) rad/s (2)2 rad/s方法感悟(1)圆锥摆类圆周运动问题,关键是确定轨道圆心、半径及有关物理量,然后再对物体进行受力分析求解。(2)当转速变化时,往往会出现一些临界状况,如绳子松弛或拉紧,绳子突然断裂,物体脱离接触面,摩擦力方向改变、达到极值,弹簧的弹力大小或方向发生变化等,要仔细分析。1. (多选)如图所示,在固定的圆锥形漏斗的光滑内壁上,有两个小球 A 和 B,质量分别为 mA和 mB,它们分别紧贴漏斗的内壁在不同的水平面上做匀速圆周运动。则以下叙述正确的是( )A.只有当 mA