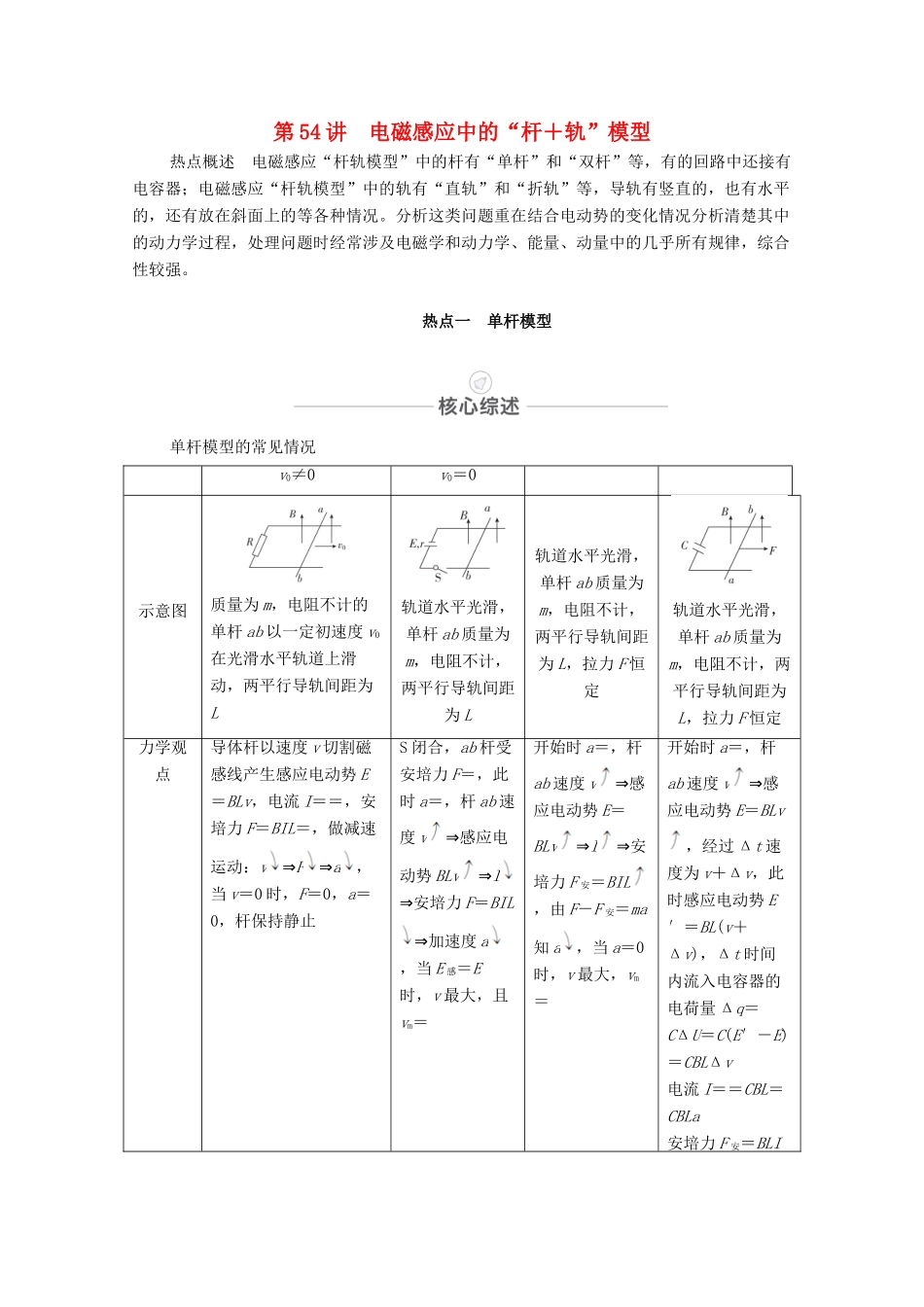
第 54 讲 电磁感应中的“杆+轨”模型热点概述 电磁感应“杆轨模型”中的杆有“单杆”和“双杆”等,有的回路中还接有电容器;电磁感应“杆轨模型”中的轨有“直轨”和“折轨”等,导轨有竖直的,也有水平的,还有放在斜面上的等各种情况。分析这类问题重在结合电动势的变化情况分析清楚其中的动力学过程,处理问题时经常涉及电磁学和动力学、能量、动量中的几乎所有规律,综合性较强。热点一 单杆模型单杆模型的常见情况v0≠0v0=0示意图质量为 m,电阻不计的单杆 ab 以一定初速度 v0在光滑水平轨道上滑动,两平行导轨间距为L轨道水平光滑,单杆 ab 质量为m,电阻不计,两平行导轨间距为 L轨道水平光滑,单杆 ab 质量为m,电阻不计,两平行导轨间距为 L,拉力 F 恒定轨道水平光滑,单杆 ab 质量为m,电阻不计,两平行导轨间距为L,拉力 F 恒定力学观点导体杆以速度 v 切割磁感线产生感应电动势 E=BLv,电流 I==,安培力 F=BIL=,做减速运动:v⇒F⇒a,当 v=0 时,F=0,a=0,杆保持静止S 闭合,ab 杆受安培力 F=,此时 a=,杆 ab 速度 v⇒感应电动势 BLv⇒I⇒安培力 F=BIL⇒加速度 a,当 E 感=E时,v 最大,且vm=开始时 a=,杆ab 速度 v⇒感应电动势 E=BLv⇒I⇒安培力 F 安=BIL,由 F-F 安=ma知 a,当 a=0时,v 最大,vm=开始时 a=,杆ab 速度 v⇒感应电动势 E=BLv,经过 Δt 速度为 v+Δv,此时感应电动势 E′=BL(v+Δv),Δt 时间内流入电容器的电荷量 Δq=CΔU=C(E′-E)=CBLΔv电流 I==CBL=CBLa安培力 F 安=BLI=CB2L2aF-F 安=ma,a=,所以杆以恒定的加速度匀加速运动图象观点能量观点动能全部转化为内能:Q=mv电源输出的电能转化为动能 W 电=mvF 做的功一部分转化为杆的动能,一部分产生电热:WF=Q+mvF 做的功一部分转化为动能,一部分转化为电场能:WF=mv2+EC注:若光滑导轨倾斜放置,要考虑导体杆受到重力沿导轨斜面向下的分力作用,分析方法与表格中受外力 F 时的情况类似,这里就不再赘述。 [例 1] 图甲、乙、丙中除导体棒 ab 可动外,其余部分均固定不动。甲图中的电容器C 原来不带电,所有导体棒、导轨电阻均可忽略,导体棒和导轨间的摩擦也不计,导体棒 ab的质量为 m。图中装置均在水平面内,且都处于方向垂直水平面(即纸面)向下的匀强磁场中,磁感应强度为 B,导轨足够长,间距为 L。今给导体棒 ab ...