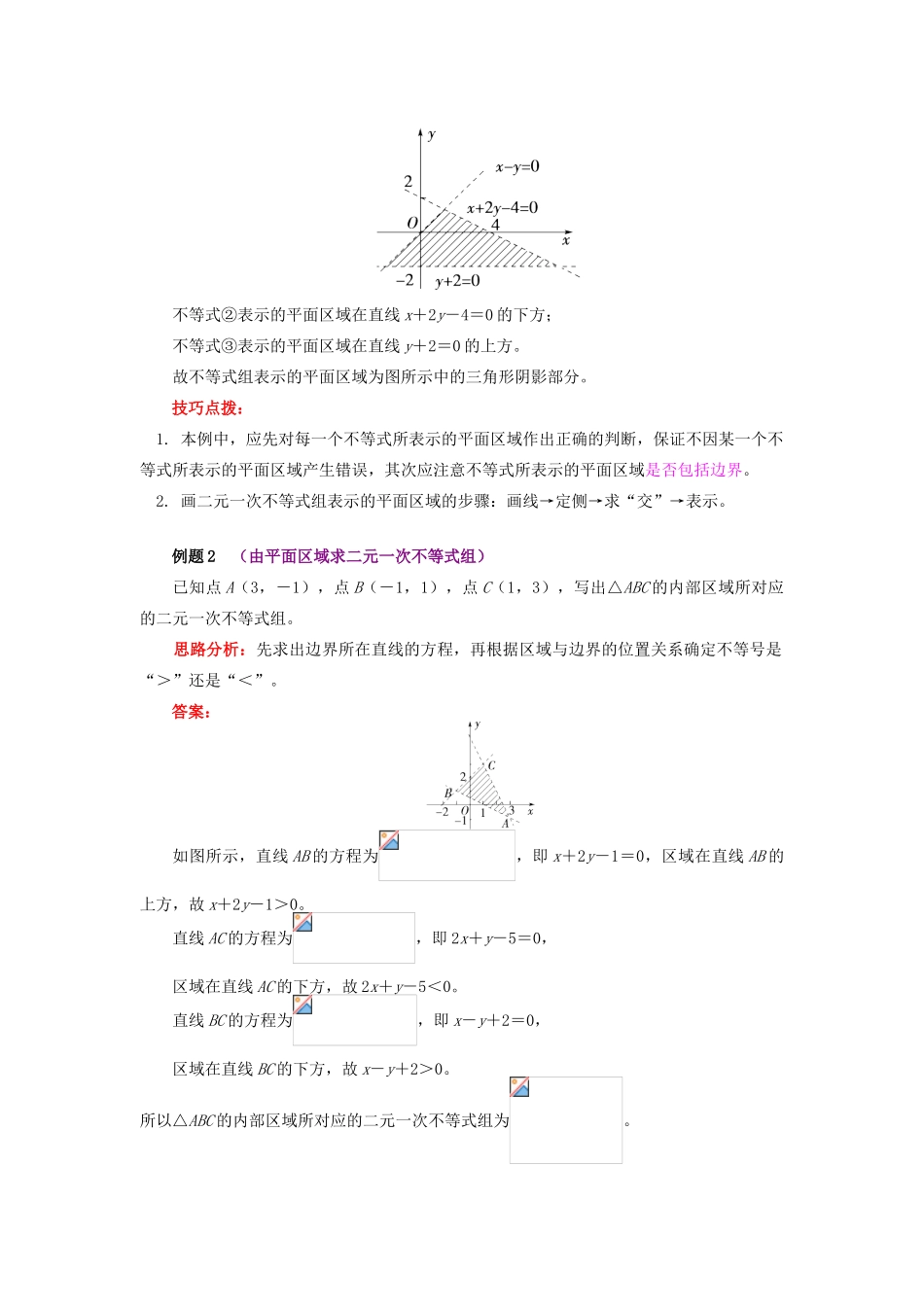
基本不等式的证明一、考点突破知识点课标要求题型说明二元一次不等式组表示的平面区域1.能从实际情境中抽象出二元一次不等式组;2.能用平面区域表示二元一次不等式组。选择题填空题正确地画出不等式组所表示的平面区域是为后面求最值的关键步骤,需要认真练习掌握。二、重难点提示重点:理解二元一次不等式组表示平面区域并能把不等式(组)所表示的平面区域画出来。难点:把实际问题抽象化,用二元一次不等式(组)表示平面区域。考点一:二元一次不等式组表示的平面区域1. 二元一次不等式组表示的平面区域,是构成不等式组的各个不等式所表示平面区域的公共部分。2. 作平面区域的步骤:(1)画线——画出不等式对应的方程所表示的直线(如果原不等式中带等号,则画成实线,否则,画成虚线);(2)定侧——将某个区域明显的特殊点的坐标代入不等式,根据“同侧同号,异侧异号”的规律确定不等式所表示的平面区域在直线的哪一侧;(3)求交——如果平面区域是由不等式组决定的,则在确定了各个不等式所表示的区域后,再求这些区域的公共部分,这个公共部分就是不等式组所表示的平面区域,俗称“直线定界,特殊点定域”。考点二:含绝对值的不等式表示的平面区域的作法(1)去绝对值符号,从而把含绝对值的不等式问题转化为普通的二元一次不等式。(2)一般采用分象限讨论区绝对值符号。(3)采用对称性可避免对绝对值的讨论。(4)在方程或不等式中,若将换成,方程或不等式不变,则这个方程或不等式所表示的图形就关于轴或轴对称。【随堂练习】若不等式组所表示的平面区域被直线 y=kx+分为面积相等的两部分,则 k 的值是 。 答案:不等式组表示的平面区域如图所示。由于直线 y=kx+过定点,因此只有直线过 AB 中点时,直线 y=kx+能平分平面区域。因为 A(1,1),B(0,4),所以 AB 中点 D。当 y=kx+过点时,+,所以 k=。思路分析:画出平面区域,显然点在已知的平面区域内,直线过定点,结合图形寻找直线平分平面区域面积的条件即可。技巧点拨:不等式组表示的平面区域是各个不等式所表示的平面区域点集的交集,画出图形后,面积关系可结合平面知识探求。例题 1 (画二元一次不等式组表示的平面区域)画出不等式组表示的平面区域。思路分析:分别画出三个不等式表示的区域→找出公共区域。答案:原不等式组等价于将(1,0)分别代入①②③的左边知不等式①表示的平面区域在直线 x-y=0 的下方;不等式②表示的...