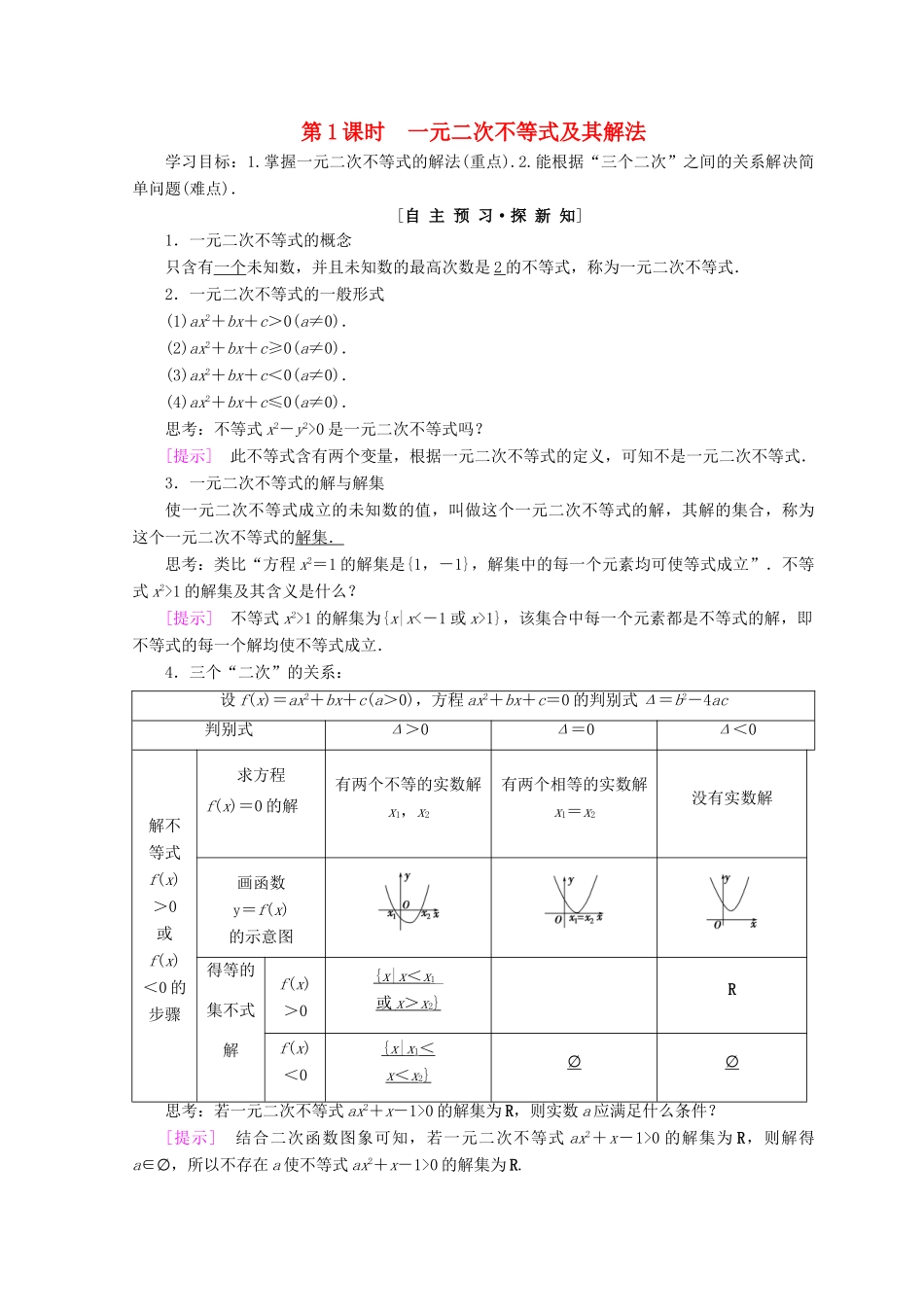
第 1 课时 一元二次不等式及其解法学习目标:1.掌握一元二次不等式的解法(重点).2.能根据“三个二次”之间的关系解决简单问题(难点).[自 主 预 习·探 新 知]1.一元二次不等式的概念只含有一个未知数,并且未知数的最高次数是 2 的不等式,称为一元二次不等式.2.一元二次不等式的一般形式(1)ax2+bx+c>0(a≠0).(2)ax2+bx+c≥0(a≠0).(3)ax2+bx+c<0(a≠0).(4)ax2+bx+c≤0(a≠0).思考:不等式 x2-y2>0 是一元二次不等式吗?[提示] 此不等式含有两个变量,根据一元二次不等式的定义,可知不是一元二次不等式.3.一元二次不等式的解与解集使一元二次不等式成立的未知数的值,叫做这个一元二次不等式的解,其解的集合,称为这个一元二次不等式的解集.思考:类比“方程 x2=1 的解集是{1,-1},解集中的每一个元素均可使等式成立”.不等式 x2>1 的解集及其含义是什么?[提示] 不等式 x2>1 的解集为{x|x<-1 或 x>1},该集合中每一个元素都是不等式的解,即不等式的每一个解均使不等式成立.4.三个“二次”的关系:设 f(x)=ax2+bx+c(a>0),方程 ax2+bx+c=0 的判别式 Δ=b2-4ac判别式Δ>0Δ=0Δ<0解不等式f(x)>0或f(x)<0 的步骤求方程f(x)=0 的解有两个不等的实数解x1,x2有两个相等的实数解x1=x2没有实数解画函数y=f(x)的示意图得等的集不式解f(x)>0{ x | x < x 1_或 x > x 2}Rf(x)<0{ x | x 1<x < x 2}∅∅思考:若一元二次不等式 ax2+x-1>0 的解集为 R,则实数 a 应满足什么条件?[提示] 结合二次函数图象可知,若一元二次不等式 ax2+x-1>0 的解集为 R,则解得a∈∅,所以不存在 a 使不等式 ax2+x-1>0 的解集为 R.[基础自测]1.思考辨析(1)mx2-5x<0 是一元二次不等式.( )(2)若 a>0,则一元二次不等式 ax2+1>0 无解.( )(3)若一元二次方程 ax2+bx+c=0 的两根为 x1,x2(x10 的解集为 R.( )[答案] (1)× (2)× (3)× (4)√ 提示:(1)错误.当 m=0 时,是一元一次不等式;当 m≠0 时,是一元二次不等式.(2)错误.因为 a>0,所以不等式 ax2+1>0 恒成立,即原不等式的解集为 R.(3)错误.当 a>0 时,ax2+bx+c<0 的解集为{x|x10 ...