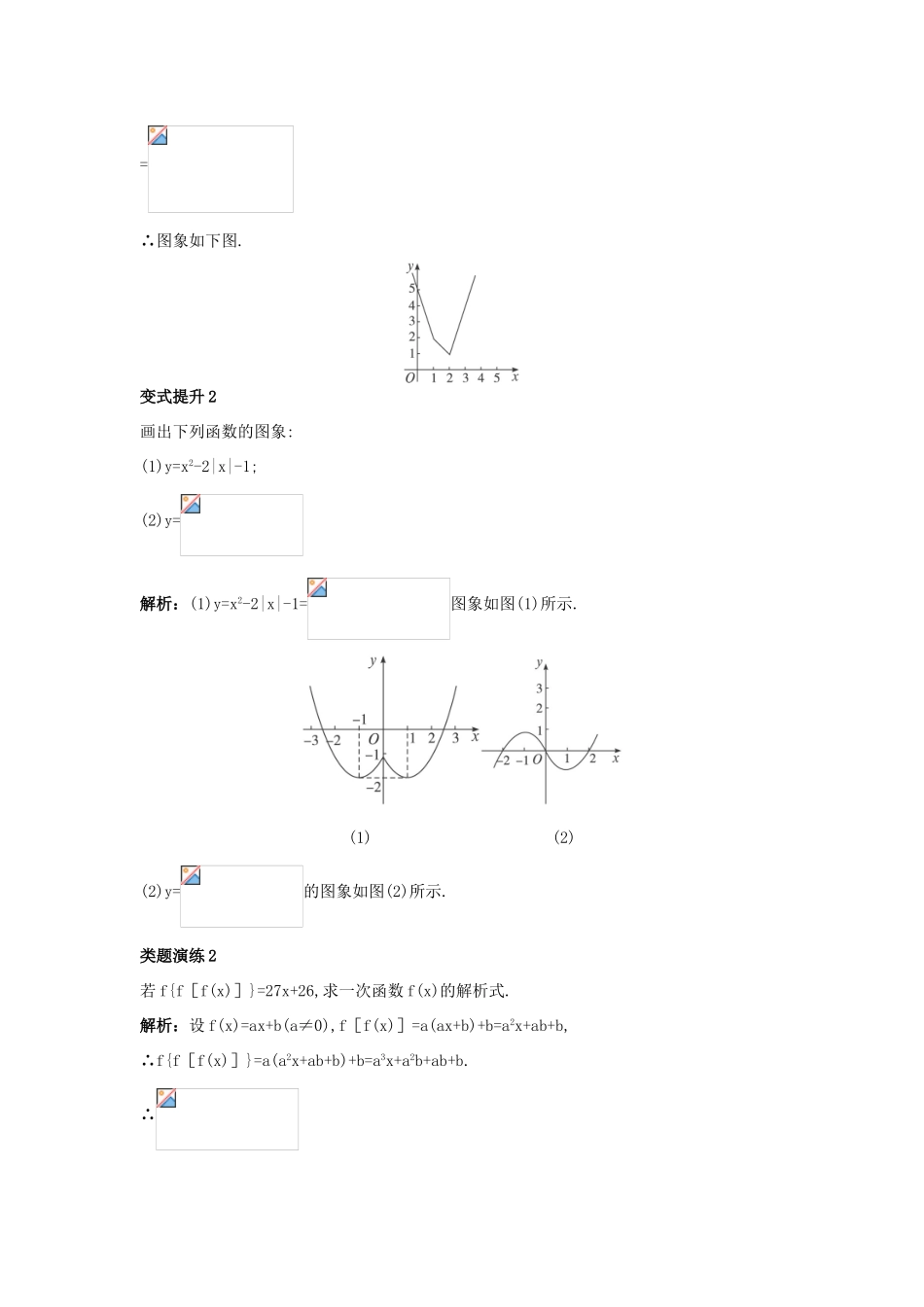
2.1.2 函数的表示方法第 1 课时函数的表示方法课堂导学三点剖析一、准确理解函数的意义,画函数的图象【例 1】作下列各函数的图象.(1)y=2x-1,x∈Z;(2)y=|x-1|.思路分析:作函数的图象关键在于明确函数图象的形状,所以可先将函数化简整理,这里即讨论 x-1 的符号,从而去掉绝对值,达到化简的目的.解:(1)这个函数的图象由一些点组成,这些点都在直线 y=2x-1 上.(∵x∈Z,∴y∈Z)这些点称为整点,如图①.(2)所给函数可写成 y=其图象是端点为(1,0)的两条射线,如图②.温馨提示 (1)求作函数图象时,一般应用描点法,根据特点,找出几个关键点即可. (2)作出函数图象,我们还可以利用它求函数的值域以及研究函数的性质.二、求函数解析式【例 2】已知 f()=,求 f(x).思路分析:要求 f(x),应把看作一个整体,采用配凑法或者换元法求出 f(x).解法一:∵f()==()2+=()2=()2-()+1,∴f(x)=x2-x+1(x≠1).解法二:设=u,则 x=,u≠1,则 f(u)=+u-1=u2-u+1,∴f(x)=x2-x+1(x≠1).温馨提示 已知复合函数 f[g(x)]的表达式时,可以用换元法求解,但要注意换元时引起的定义域的变化,最后结果注明所求函数的定义域.三、对 y=f(x)对应法则的理解【例 3】已知函数 f(x)=求 f(2)、f(3)、f(4).思路分析:所给函数用两个等式定义,第一个等式首先给出自变量的初始值对应的函数值,然后由这个函数值用第二个等式依次递推地计算下一个函数值.解:f(2)=1+f(2-1)=1+f(1)= ,f(3)=1+f(3-1)=1+f(2)=,f(4)=1+f(4-1)=1+f(3)=.温馨提示 上述运算方法叫递归运算,运用递归运算时,要弄清各部分的关系,依次代入即可.解题时要对 f(n)理解到位.各个击破类题演练 1作出函数 y=|x-1|+2|x-2|的图象.解析:y=|x-1|+2|x-2|=∴图象如下图.变式提升 2画出下列函数的图象:(1)y=x2-2|x|-1;(2)y=解析:(1)y=x2-2|x|-1=图象如图(1)所示.(1) (2)(2)y=的图象如图(2)所示.类题演练 2若 f{f[f(x)]}=27x+26,求一次函数 f(x)的解析式.解析:设 f(x)=ax+b(a≠0),f[f(x)]=a(ax+b)+b=a2x+ab+b,∴f{f[f(x)]}=a(a2x+ab+b)+b=a3x+a2b+ab+b.∴∴∴f(x)=3x+2,经检验成立.变式提升 2已知 f(x)为二次函数,且 f(x+1)+f(x-1)=2x2-4x,求 f(x)的表达式.解析:设 f(x)=ax2+bx+c(a≠0),则 f(x+1)+f(x-1)=a(x+1)2+b(x+1)+c+a(x-1)2+b(x-1)+c=2ax2+2bx+2a+2c=2x2-4x.∴解得∴f(x)=x2-2x-1.类题演练 3已知函数 f(x)=,那么 f(1)+f(2)+f()+f(3)+f()=.解析:∵f()==,∴f()+f(x)=1.∴原式=+1+1=.答案:变式提升 3已知 f(0)=1,f(a-b)=f(a)-b(2a-b+1),求 f(x).解析:令 a=0,则 f(-b)=f(0)-b(-b+1)=1+b(b-1)=b2-b+1,再令-b=x,得 f(x)=x2+x+1.