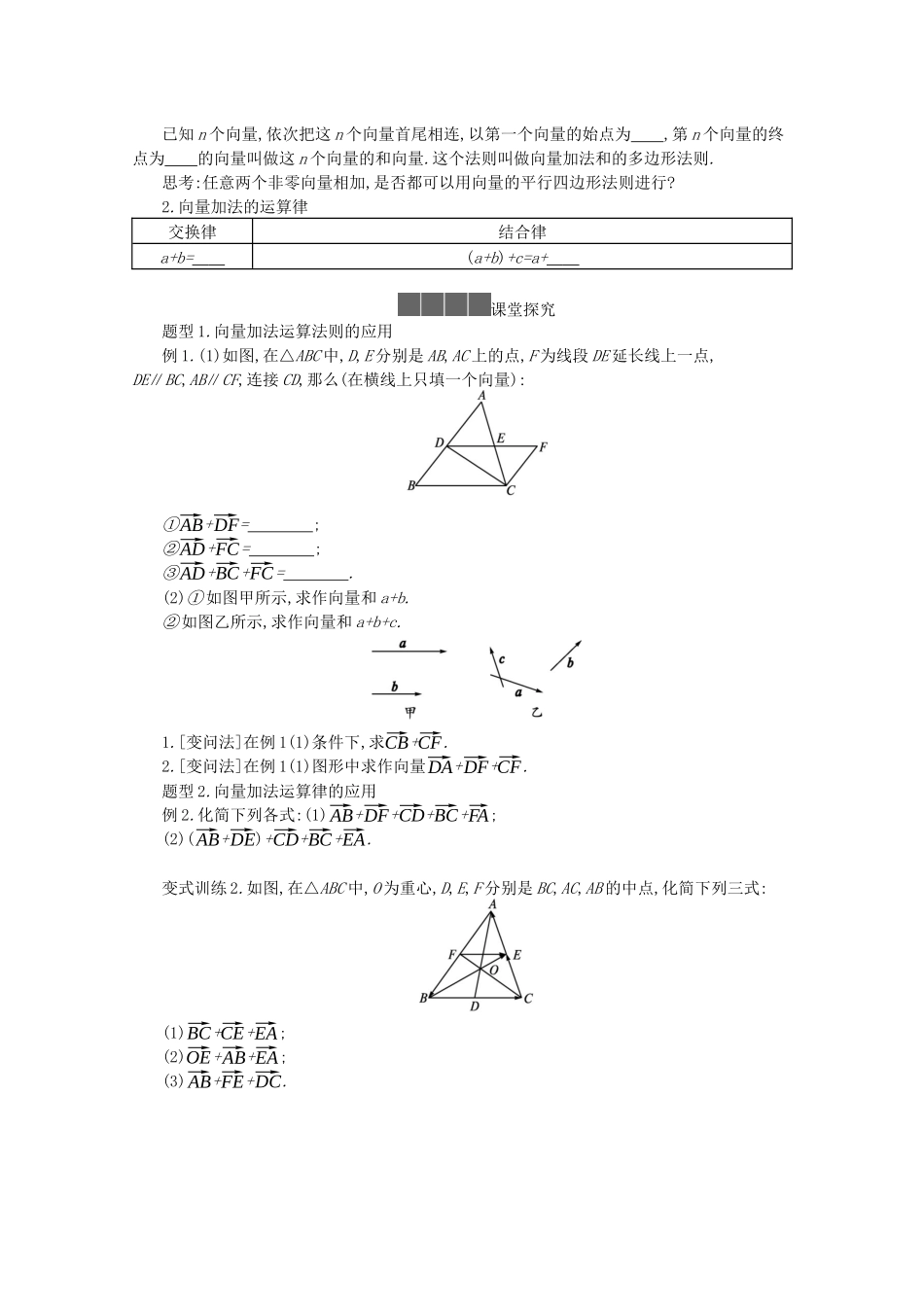
6.1.2 向量的加法学习目标学习目标核心素养1.掌握向量加法的运算,并理解其几何意义.(重点)2.理解向量加法的三角形法则、平行四边形法则、多边形法则的适用范围,并能应用向量加法的运算律进行相关运算.(难点)1.通过向量加法的三角形法则和平行四边形法则的学习,培养直观想象.2.通过学习向量加法的运算律,培养逻辑推理.自主预习有两条拖轮牵引一艘驳船,它们的牵引力分别是 F1=3 000 牛,F2=2 000 牛,牵绳之间的夹角θ=60°.如果只用一条拖轮来牵引,产生的效果跟原来的相同,试求出这条拖轮的牵引力的大小和方向.一、预习教材 P137~141的内容,思考以下问题:1.某人从 A 到 B,再从 B 顺着原来的方向到 C,此人总的位移是什么?2.湖上三个景点 O,A,B,游艇将游客从景点 O 送至景点 A,位移是什么?再将游客从景点 A送至景点 B,位移是什么?两次位移后游艇总的位移是什么?这三个位移之间的关系是什么?3.平面上任意两个向量的和怎么求?二、1.向量的加法法则(1)三角形法则一般地,平面上任意给定两个向量 a,b,在该平面内任取一点 A,作⃗AB=a,⃗BC=b,作出向量⃗AC,则向量⃗AC称为 a 与 b 的和(或和向量),记作 ,即 a+b=⃗AB+⃗BC= . 上述求两个向量和的作图方法,叫做向量加法的三角形法则.对于零向量与任一向量 a 的和,有 a+0= + = . 向量 a,b 的模与 a+b 的模的关系:||a|-|b||≤|a+b|≤|a|+|b|.(2)平行四边形法则平面上任意给定两个不共线的向量 a,b,在该平面内任取一点 A,作⃗AB=a,⃗AD=b,则 A,B,D三点不共线,以⃗AB,⃗AD为邻边作平行四边形 ABCD,则对角线上的向量⃗AC= .这个法则叫做向量加法的平行四边形法则. (3)多边形法则已知 n 个向量,依次把这 n 个向量首尾相连,以第一个向量的始点为 ,第 n 个向量的终点为 的向量叫做这 n 个向量的和向量.这个法则叫做向量加法和的多边形法则. 思考:任意两个非零向量相加,是否都可以用向量的平行四边形法则进行?2.向量加法的运算律交换律结合律a+b= (a+b)+c=a+ 课堂探究题型 1.向量加法运算法则的应用例 1.(1)如图,在△ABC 中,D,E 分别是 AB,AC 上的点,F 为线段 DE 延长线上一点,DE∥BC,AB∥CF,连接 CD,那么(在横线上只填一个向量):①⃗AB+⃗DF= ; ②⃗AD+⃗FC= ; ③⃗AD+⃗BC+⃗FC= . (2)① 如图甲所示,求作向量和 a+b.② 如图乙所示,求作向量和 a+b+c.1.[变问法]在例 1(1)条件下,求⃗CB+⃗CF.2.[变问法]在例 1(1)图形中求作向量⃗DA+⃗D...